题目内容

20．自主招生，是高校选拔录取工作改革的重要环节，通过高考自主招生笔试和面试之后，可以得到相应的高考降分政策；某高中高一学生共有1000人，其中城填初中毕业生750名（称为“城填生“），农村初中毕业生250人（称为“农村生“）；为了摸清学生是否愿意参加自主招生，以便安排自主招生培训，拟采用分层抽样的方法抽取100名学生进行调查；
（1）试完成下列2×2联表，并分析是否有95%以上的把握说“是否愿意参加自主招生“与生源有关．
愿意参加不愿意参加合计
城填生502575
农村生101525
合计6040100
（2）现对愿意参加自主招生的同学组织摸底考试，考试题共有5道题，每题20分，对于这5道题，考生“高富帅”完全会答的有3道，不完全会的有2道，不完全会的每道题她得分S的概率满足：SKIPIF 1＜0，假设解答各题之间没有影响．
①对于一道不完全会的题，求“高富帅”得分的均值E（s）；
②试求“高富帅”在本次摸底考试中总得分的数学期望．
参考数据：
P（K2≥k0）0.100.050.0250.0100.0050.001
k02.7063.8415.0246.6357.87910.828
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d）

分析 （1）根据题意填写2×2列联表，计算K2，对照数表得出结论；
（2）①由S的所有可能取值计算对应的概率值即可；
②计算对应的分布列与期望值即可．

解答 解：（1）根据题意填写2×2列联表如下：

利用时间充分利用时间不充分总计
走读生502575
住宿生101525
总计6040100
计算K2=$\frac{100×（50×15-25×10）2}{75×25×40×60}$≈5.556，
由于K2＞3.841，所以有95%的把握认为“是否愿意参加自主招生“与生源有关；…（6分）
（2）①S的所有可能取值为6，12，18且P（S=6）=$\frac{1}{2}$，P（S=12）=$\frac{1}{3}$，P（S=18）=$\frac{1}{6}$，
E（S）=6×$\frac{1}{2}$+12×$\frac{1}{3}$+18×$\frac{1}{6}$=10，
即“高富帅”得分的均值10分…（8分）
②设不完全会的2道题的最后得分为X，总得分为Y，则Y=60+X；
X的所有可能取值为12，18，24，30，36；
P（X=12）=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$，
P（X=18）=2×$\frac{1}{2}$×$\frac{1}{3}$=$\frac{1}{3}$，
P（X=24）=$\frac{1}{3}$×$\frac{1}{3}$+2×$\frac{1}{2}$×$\frac{1}{6}$=$\frac{5}{18}$，
P（X=30）=2×$\frac{1}{3}$×$\frac{1}{6}$=$\frac{1}{9}$，
P（X=36）=$\frac{1}{6}$×$\frac{1}{6}$=$\frac{1}{36}$，
∴EX=12×$\frac{1}{4}$+18×$\frac{1}{3}$+24×$\frac{5}{18}$+30×$\frac{1}{9}$+36×$\frac{1}{36}$=20，
EY=60+EX=80；
∴“高富帅”在本次摸底考试中总得分的数学期望为80分；
（若考生用其它方法得到正确结果同样赋分）…（12分）

点评 本题考查了独立性检验与古典概型的概率与分布列、期望问题，是综合性题目．

练习册系列答案
相关题目
10．如图，给定由10个点（任意相邻两点距离为1，）组成的正三角形点阵，在其中任意取三个点，以这三个点为顶点构成的正三角形的个数是（　　）
A．12B．13C．15D．16
11．抛物线y2=20x的焦点到准线的距离是（　　）
A．5B．10C．15D．20
8．如果方程Ax+By+C=0表示的直线是x轴，则A、B、C满足（　　）
A．A•C=0B．B≠0C．B≠0且A=C=0D．A•C=0且B≠0
15．已知α，β是两个不同的平面，l，m是两条不同直线，l⊥α，m?β．给出下列命题：
①α∥β⇒l⊥m；②α⊥β⇒l∥m；③m∥α⇒l⊥β；  ④l⊥β⇒m∥α．
其中正确的命题是①④． （填写所有正确命题的序号）．
5．如图，正四面体ABCD的棱长为1，点E是棱CD的中点，则$\overrightarrow{AE}$•$\overrightarrow{AB}$=（　　）
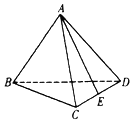
A．-$\frac{1}{4}$B．-$\frac{1}{2}$C．$\frac{1}{4}$D．$\frac{1}{2}$
12．近年来，某地雾霾污染指数达到重度污染级别．经环保部门调查，该地工厂废气排放污染是形成雾霾的主要原因．某科研单位进行了科技攻关，将工业废气中的某些成分转化为一中可利用的化工产品．已知该项目每年投入资金3000万元，设每年处理工厂废气量为x万升，每万升工厂废气处理后得到可利用的化工产品价值为c（x）万元，其中c（x）=$\left\{\begin{array}{l}{-3x+\frac{20}{x}+192，0＜x≤50}\\{-\frac{7200}{{x}^{2}}+\frac{3640}{x}-2，x＞50}\end{array}\right.$．设该单位的年利润为f（x）（万元）．
（I）求年利润f（x）（万元）关于处理量x（万升）的函数表达式；
（II）该单位年处理工厂废气量为多少万升时，所获得的利润最大，并求出最大利润？
9．在△ABC中，a=2，$B=\frac{π}{3}$，△ABC的面积等于$\frac{\sqrt{3}}{2}$，则b等于（　　）
A．$\frac{\sqrt{3}}{2}$B．1C．$\sqrt{3}$D．2
10．不等式选讲已知函数f（x）=|2x+a|-a
（1）当a=2时，求不等式f（x）≤6的解集；
（2）设函数g（x）=|2x-1|，当x∈R时f（x）+g（x）≥3，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网