题目内容
7.函数$f(x)=[{\frac{x+1}{2}}]-[{\frac{x}{2}}](x∈N)$的值域为{0,1}.(其中[x]表示不大于x的最大整数,例如[3.15]=3,[0.7]=0.)分析 由题设中的定义,可对x分区间讨论,设m表示整数,综合此四类即可得到函数的值域
解答 解:设m表示整数.
①当x=2m时,[$\frac{x+1}{2}$]=[m+0.5]=m,[$\frac{x}{2}$]=[m]=m.
∴此时恒有y=0.
②当x=2m+1时,[$\frac{x+1}{2}$]=[m+1]=m+1,[$\frac{x}{2}$]=[m+0.5]=m.
∴此时恒有y=1.
③当2m<x<2m+1时,
2m+1<x+1<2m+2
∴m<$\frac{x}{2}$<m+0.5
m+0.5<$\frac{x+1}{2}$<m+1
∴[$\frac{x}{2}$]=m,[$\frac{x+1}{2}$]=m
∴此时恒有y=0
④当2m+1<x<2m+2时,
2m+2<x+1<2m+3
∴m+0.5<$\frac{x}{2}$<m+1
m+1<$\frac{x+1}{2}$<m+1.5
∴此时[$\frac{x}{2}$]=m,[$\frac{x+1}{2}$]=m+1
∴此时恒有y=1.
综上可知,y∈{0,1}.
故答案为{0,1}.
点评 此题是新定义一个函数,根据所给的规则求函数的值域,求解的关键是理解所给的定义,一般从函数的解析式入手,要找出准确的切入点,理解[x]表示数x的整数部分,考察了分析理解,判断推理的能力及分类讨论的思想

练习册系列答案
相关题目
18.已知函数$f(x)=\left\{\begin{array}{l}lnx,x>1\\{2^{-x+1}},x≤1\end{array}\right.$,若方程$f(x)-ax=\frac{5}{2}$有3个不同的解,则a的取值范围是( )
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
15.函数$y=2\sqrt{2}sin(ωx+φ)$(其中ω>0,0<φ<π)的图象的一部分如图所示,则( )
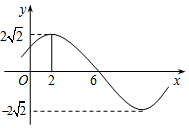

| A. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{3π}{4}$ | B. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{π}{4}$ | C. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{π}{2}$ | D. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{3π}{4}$ |
16.函数y=xlnx的最小值为( )
| A. | -e-1 | B. | -e | C. | e2 | D. | -$\frac{10}{3}$ |
13.已知2弧度的圆心角所对的半径长为2,那么这个圆心角所对的弧长是( )
| A. | 2 | B. | sin2 | C. | $\frac{2}{sin1}$ | D. | 4 |