题目内容
13.在区间[0,1]上随机选取两个数x和y,则y>3x的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |
分析 由题意,求出两个变量对应的区域面积,利用面积比求概率.
解答 解:在区间[0,1]上随机选取两个数x和y,
对应的区间为边长为1 的正方形,面积为1,
在此条件下满足y>3x的区域面积为$\frac{1}{2}×1×\frac{1}{3}$=$\frac{1}{6}$,
所以所求概率为$\frac{1}{6}$,
故选A.
点评 本题考查了几何概型的概率求法;由于两个变量,所以利用面积比求概率;明确几何测度是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名五年级学生进行了问卷调查得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为$\frac{4}{15}$
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)若常喝碳酸饮料且肥胖的学生中有2名女生,现从常喝碳酸饮料且肥胖的学生中抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 合计 | 30 |
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)若常喝碳酸饮料且肥胖的学生中有2名女生,现从常喝碳酸饮料且肥胖的学生中抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5.已知a,b∈R,定义运算“?”:a?b=$\left\{\begin{array}{l}{aa-b≤1}\\{ba-b>1}\end{array}\right.$,函数f(x)=(x2-2)?(x-1),x∈R,若方程f(x)-a=0只有两个不同实数根,则实数a的取值范围是( )
| A. | [-2,-1]∪(1,2) | B. | (-2,-1]∪(1,2] | C. | [-2,-1]∪[1,2] | D. | (-2,-1]∪(1,2) |




 在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.
在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.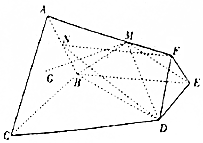 如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.
如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.