题目内容
3.已知点P($\sqrt{3}$,1),Q(cosx,sinx),O为坐标原点,函数f(x)=$\overrightarrow{OP}$•$\overrightarrow{QP}$.(Ⅰ)求函数f(x)的解析式及f(x)的最小正周期;
(Ⅱ)若A为△ABC的内角,f(A)=4,BC=3,求△ABC周长的最大值.
分析 (Ⅰ)利用向量的数量积以及两角和与差的三角函数化简函数的解析式,然后求解f(x)的最小正周期;
(Ⅱ)利用函数的解析式求解A,然后利用余弦定理求解即可,得到bc的范围,然后利用基本不等式求解最值.
解答 解:(Ⅰ)f(x)=$\overrightarrow{OP}$•$\overrightarrow{QP}$=($\sqrt{3}$,1)•($\sqrt{3}$-cosx$\sqrt{3}$,1-sinx)
=-$\sqrt{3}$cosx-sinx+4=-2sin(x+$\frac{π}{3}$)+4,
f(x)的最小正周期T=$\frac{2π}{2}$=π;
(Ⅱ)∵f(A)=4,∴A=$\frac{2π}{3}$,
又∵BC=3,
∴9=(b+c)2-bc.
∵bc≤$\frac{(b+c)^{2}}{4}$,
∴$\frac{3(b+c)^{2}}{4}≤9$,
∴b+c≤2$\sqrt{3}$,当且仅当b=c取等号,
∴三角形周长最大值为3+2$\sqrt{3}$.
点评 本题考查向量的数量积以及两角和与差的三角函数,三角函数的周期,基本不等式以及余弦定理的应用,考查计算能力.

练习册系列答案
相关题目
13.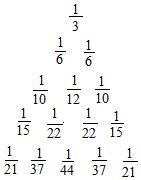 如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依次规律A(8,2)为( )
如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依次规律A(8,2)为( )
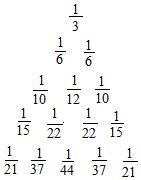 如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依次规律A(8,2)为( )
如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依次规律A(8,2)为( )| A. | $\frac{1}{45}$ | B. | $\frac{1}{86}$ | C. | $\frac{1}{122}$ | D. | $\frac{1}{167}$ |
14.已知x,y满足约束条件$\left\{\begin{array}{l}{x-y-2≤0}&{\;}\\{ax+y≥4}&{\;}\\{x-2y+3≥0}&{\;}\end{array}\right.$,目标函数z=2x-3y的最大值是2,则实数a=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 4 |
11.已知函数f(x)是定义在R上的可导函数,其导函数为f′(x),则命题P:“?x1,x2∈R,且x1≠x2,|$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$|<2017”是命题Q:“?x∈R,|f′(x)|<2017”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.定义在R上的函数f(x)满足f(x)=$\left\{\begin{array}{l}{log_2}(8-x),x≤0\\ f(x-1),x>0\end{array}$则f(3)=( )
| A. | 3 | B. | 2 | C. | log29 | D. | log27 |
12.已知曲线C:$\left\{\begin{array}{l}x=\frac{{\sqrt{2}}}{2}t\\ y=a+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数),A(-1,0),B(1,0),若曲线C上存在点P满足$\overrightarrow{AP}$•$\overrightarrow{BP}$=0,则实数a的取值范围为( )
| A. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ | B. | [-1,1] | C. | $[{-\sqrt{2},\sqrt{2}}]$ | D. | [-2,2] |
13.在区间[0,1]上随机选取两个数x和y,则y>3x的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |