题目内容
已知函数f(x)=
,若关于x的方程[f(x)]2+bf(x)+2=0有四个不同的正根,则b的取值范围是( )
| 1 |
| |x-1| |
A、(-∞,-2
| ||||
B、(-3,-2
| ||||
C、(-3,2
| ||||
D、(-2
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:利用换元法,将方程转化为关于t的一元二次方程,根据根的分布,利用数形结合即可得到结论.
解答:
 解:设t=f(x)=
解:设t=f(x)=
,作出函数f(x)的图象如图:
则方程等价为t2+bt+2=0,
若x的方程[f(x)]2+bf(x)+2=0有四个不同的正根,
则等价为t2+bt+2=0存在两个不同的根t1,t2,且t1>1,t2>1,
设g(t)=t2+bt+2,
则满足条件
,
即
,
则
,
解得-3<b<-2
,
故选:B
 解:设t=f(x)=
解:设t=f(x)=| 1 |
| |x-1| |
则方程等价为t2+bt+2=0,
若x的方程[f(x)]2+bf(x)+2=0有四个不同的正根,
则等价为t2+bt+2=0存在两个不同的根t1,t2,且t1>1,t2>1,
设g(t)=t2+bt+2,
则满足条件
|
即
|
则
|
解得-3<b<-2
| 2 |
故选:B
点评:本题主要考查方程根的个数的应用,利用换元法以及数形结合,将方程转化为一元二次方程是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
A、B是双曲线
-
=1右支上的两点,若弦AB的中点到Y轴的距离是4,则|AB|的最大值为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、2 | B、4 | C、6 | D、8 |
已知“渐升数”是指每一位数字比其左边的数字大的正整数(如236),那么任取一个三位数,它是渐升数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
直线x+
y-m=0与圆x2+y2=1在第一象限内有两个不同的交点,则m的取值范围是( )
| 3 |
| A、(1,2) | ||
B、(
| ||
C、(1,
| ||
D、(
|
某几何体的三视图如图所示,则该几何体的表面积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
已知0<b<1,0<α<
,x=(sinα)logbsinα,y=(cosα)logbcosα,z=(sinα)logbcosα则三数的大小关系是( )
| π |
| 4 |
| A、x<y<z |
| B、z<x<y |
| C、x<z<y |
| D、y<z<x |
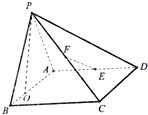 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD、PC的中点.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD、PC的中点.