题目内容
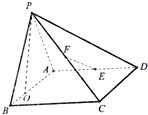 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD、PC的中点.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD、PC的中点.(1)求证:EF∥平面PAB,EF⊥平面PBC;
(2)若直线PC与平面ABCD所成角为
| π |
| 4 |
考点:直线与平面垂直的判定,直线与平面平行的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)取BP的中点M,FM∥BC,且FM∥PE,从而四边形AMFE是平行四边形,由此能证明EF∥平面PAB;由PA=AB,得AM⊥PB,EF⊥PB,由线面垂直得BC⊥AB,从而BC⊥平面PAB,由此能证明EF⊥平面PBC.
(2)作PO⊥AB=O,则PO⊥平面ABCD,连结OC,BC中点G,连EG、FG,由已知得∠FGE即为所求二面角的平面角,由此能求出BO、PB长及二面角P-BC-E的余弦值.
(2)作PO⊥AB=O,则PO⊥平面ABCD,连结OC,BC中点G,连EG、FG,由已知得∠FGE即为所求二面角的平面角,由此能求出BO、PB长及二面角P-BC-E的余弦值.
解答:
(1)证明:取BP的中点M,FM∥BC,且FM∥PE,
∴四边形AMFE是平行四边形,
∴AM∥EF,又EF在平面PAB外,EF∥平面PAB,
由PA=AB,得AM⊥PB,EF⊥PB,
∵平面PAB⊥平面ABCD,BC⊥AB,
∴BC⊥平面PAB,∴BC⊥AM,∴BC⊥EF,
∴EF⊥平面PBC.
(2)解:作PO⊥AB=O,则PO⊥平面ABCD,
连结OC,则∠PCO=
,
∴PO=OC,设AO=x,则
=
,
得到x=2,
则BC中点G,连EG、FG,则由(1)知BC⊥平面EFG,
∠FGE即为所求二面角的平面角,
在△PAB中,PB=
,PA=AB=3,
∴cos∠FGE=
.
∴四边形AMFE是平行四边形,
∴AM∥EF,又EF在平面PAB外,EF∥平面PAB,
由PA=AB,得AM⊥PB,EF⊥PB,
∵平面PAB⊥平面ABCD,BC⊥AB,
∴BC⊥平面PAB,∴BC⊥AM,∴BC⊥EF,
∴EF⊥平面PBC.
(2)解:作PO⊥AB=O,则PO⊥平面ABCD,
连结OC,则∠PCO=
| π |
| 4 |
∴PO=OC,设AO=x,则
| 9-x2 |
| 4+(3-x)2 |
得到x=2,
则BC中点G,连EG、FG,则由(1)知BC⊥平面EFG,
∠FGE即为所求二面角的平面角,
在△PAB中,PB=
| 6 |
∴cos∠FGE=
| ||
| 6 |
点评:本题考查直线与平面平行的证明,考查直线与平面垂直的证明,考查线段长的求法,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,若关于x的方程[f(x)]2+bf(x)+2=0有四个不同的正根,则b的取值范围是( )
| 1 |
| |x-1| |
A、(-∞,-2
| ||||
B、(-3,-2
| ||||
C、(-3,2
| ||||
D、(-2
|
 已知椭圆C1:
已知椭圆C1: 某校开设有数学史选修课,为了解学生对数学史的掌握情况,举办了数学史趣味知识竞赛,现将成绩统计如下.请你根据尚未完成任务的频率分布表和局部污损的频率分布直方图,解答下列问题:
某校开设有数学史选修课,为了解学生对数学史的掌握情况,举办了数学史趣味知识竞赛,现将成绩统计如下.请你根据尚未完成任务的频率分布表和局部污损的频率分布直方图,解答下列问题: