题目内容
设抛物线C:y2=2px(p>0)的焦点为F,准线为l,M∈C,以M为圆心的圆M与l,相切于点Q,Q的纵坐标为
p,E(5,0)是圆M与x轴除F外的另一个交点
(Ⅰ)求抛物线C与圆M的方程;
(Ⅱ)已知直线n:y=k(x-1)(k>0),n与C交于A,B两点,n与l交于点D,且|FA|=|FD|,求△ABQ的面积.
| 3 |
(Ⅰ)求抛物线C与圆M的方程;
(Ⅱ)已知直线n:y=k(x-1)(k>0),n与C交于A,B两点,n与l交于点D,且|FA|=|FD|,求△ABQ的面积.
考点:直线与圆锥曲线的关系,圆的标准方程,抛物线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由抛物线的定义,结合M∈C,确定M的坐标,根据M是线段EF垂直平分线上的点,建立方程,即可求抛物线C与圆M的方程:
(Ⅱ)根据|FA|=|FD|,求出直线n的方程,与抛物线方程联立,求出A,B的坐标,进而求出|AB|,Q到直线n的距离,即可求△ABQ的面积.
(Ⅱ)根据|FA|=|FD|,求出直线n的方程,与抛物线方程联立,求出A,B的坐标,进而求出|AB|,Q到直线n的距离,即可求△ABQ的面积.
解答:
解:(Ⅰ)由抛物线的定义知,圆M经过焦点F(
,0),Q(-
,
p),点M的纵坐标为
p,
∵M∈C,∴M(
p,
p),|MF|=2p,
由题意,M是线段EF垂直平分线上的点,
∴
p=
,
∴p=2,
∴抛物线C:y2=4x,圆M的方程:(x-3)2+(y-2
)2=16;
(Ⅱ)由
,可得y=-2k,∴D(-1,-2).
直线n:y=k(x-1)代入抛物线方程,整理可得ky2-4y-4k=0(k>0),
∴y=
,
∵|FA|=|FD|,∴
=2k,
∴k=
,
∴A(3,2
),B(
,
),直线n:y=
(x-1),Q(-1,2
),
则|AB|=
,Q到直线n的距离为d=2
,
∴△ABQ的面积S=
|AB|d=
.
| p |
| 2 |
| p |
| 2 |
| 3 |
| 3 |
∵M∈C,∴M(
| 3 |
| 2 |
| 3 |
由题意,M是线段EF垂直平分线上的点,
∴
| 3 |
| 2 |
| ||
| 2 |
∴p=2,
∴抛物线C:y2=4x,圆M的方程:(x-3)2+(y-2
| 3 |
(Ⅱ)由
|
直线n:y=k(x-1)代入抛物线方程,整理可得ky2-4y-4k=0(k>0),
∴y=
2±2
| ||
| k |
∵|FA|=|FD|,∴
2+2
| ||
| k |
∴k=
| 3 |
∴A(3,2
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
则|AB|=
| 16 |
| 3 |
| 3 |
∴△ABQ的面积S=
| 1 |
| 2 |
16
| ||
| 3 |
点评:本题考查抛物线的定义,考查抛物线与圆的方程,考查直线与抛物线的位置关系,考查三角形面积的计算,属于中档题.

练习册系列答案
相关题目
A={x|x2≥4},B={x|2x=
},则A∩B=( )
| 1 |
| 4 |
| A、{2} |
| B、(-∞,-2] |
| C、[2,+∞) |
| D、{-2} |
 坚持锻炼一小时,健康成长每一天.某校为调查高中学生在校参加体育活动的时间,随机抽取了100名高中学生进行调查,其中女学生有55名.上面是根据调查结果绘制的学生日均体育锻炼时间的频率分布直方图:
坚持锻炼一小时,健康成长每一天.某校为调查高中学生在校参加体育活动的时间,随机抽取了100名高中学生进行调查,其中女学生有55名.上面是根据调查结果绘制的学生日均体育锻炼时间的频率分布直方图: 如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.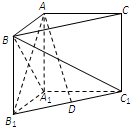 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.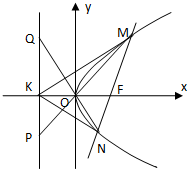 如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.
如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.