题目内容
设f（x）是在R上的奇函数，且为减函数，f（2a2+a+1）+f（2a-3a2-1）＜0，求a的取值范围．
考点：奇偶性与单调性的综合
专题：计算题,函数的性质及应用
分析：先根据函数是定义在R上的奇函数，把不等式f（2a2+a+1）+f（2a-3a2-1）＜0变形为f（2a2+a+1）＜-f（2a-3a2-1），再根据f（x）在R上是减函数，去函数符号，再解关于a的二次不等式即可．
解答：
解：∵f（2a2+a+1）+f（2a-3a2-1）＜0，∴f（2a2+a+1）＜-f（2a-3a2-1），
又∵f（x）为奇函数，∴f（2a2+a+1）＜f（-2a+3a2+1），
∵f（x）在R上是减函数，∴2a2+a+1＞-2a+3a2+1，
解得0＜a＜3．
又∵f（x）为奇函数，∴f（2a2+a+1）＜f（-2a+3a2+1），
∵f（x）在R上是减函数，∴2a2+a+1＞-2a+3a2+1，
解得0＜a＜3．
点评：本题考查了函数的奇偶性与单调性，做题时应认真分析，找到切入点．
练习册系列答案
相关题目
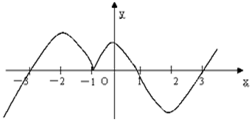已知函数y=f（x）的导函数y=f′（x）图象如图所示