Question

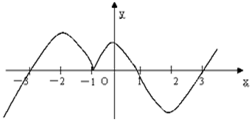已知函数y=f（x）的导函数y=f′（x）图象如图所示
①函数y=f（x）在x=-3，x=3处有极小值
②函数y=f（x）在区间（0，1）上单调递减
③函数y=f（x）在区间（2，3）上单调递增
④函数y=f（x）在x=-1，x=1处有极大值
⑤函数y=f（x）在区间（-3，1）上单调递增
则以上结论正确的序号是：

 

．

Answer 1

考点：利用导数研究函数的单调性

专题：导数的概念及应用

分析：结合函数的图象得出：f（x）在（-∞，-3）递减，在（-3，1）递增，f（x）在（1，3）递减，在（3，+∞）递增，从而逐项判断，进而得出答案．

解答： 解：∵在区间（-∞，-3）上，f′（x）＜0，在（-3，1）上，f（x）≥0，
∴f（x）在（-∞，-3）递减，在（-3，1）递增，
∴f（x）_极小值=f（-3），
∵在区间（1，3）上，f′（x）＜0，在（3，+∞）上，f′（x）＞0，
∴f（x）在（1，3）递减，在（3，+∞）递增，
∴f（x）_极小值=f（3），
故①⑤正确，②③④错误；
故答案为：①⑤．

点评：本题考查了函数的单调性，函数的极值问题，考查数形结合思想，是一道基础题．