题目内容
设函数f(x)=
,若函数y=f(x)-x恰有三个零点,则实数m的取值范围的( )
|
| A、[-1,2) |
| B、[1,2] |
| C、[2,+∞) |
| D、(-∞,-1] |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:设函数g(x)=
,要使函数y=f(x)-x恰有三个零点,必须使y=2-x有零点并且y=x2+3x+2有两个零点,从而得到m<2并且m≥-1.
|
解答:
解:构造函数g(x)=
,
要使函数y=f(x)-x恰有三个零点,
必须使函数y=2-x有零点,并且函数y=x2+3x+2有两个零点,从而得到m<2并且m≥-1.
故选A.
|
要使函数y=f(x)-x恰有三个零点,
必须使函数y=2-x有零点,并且函数y=x2+3x+2有两个零点,从而得到m<2并且m≥-1.
故选A.
点评:本题考查了函数的零点个数,关键是构造新函数,结合每一段的函数解析式及其零点个数得到参数范围,属于中档题.

练习册系列答案
相关题目
函数f(x)=x3+ax2+x在(0,+∞)有两个极值点,则实数a的取值范围是( )
A、(-∞,
| ||||
B、(-
| ||||
C、(
| ||||
D、(-∞,-
|
已知点A(1,2),B(3,2),以线段AB为直径作圆C,则直线l:x+y-3=0与圆C的位置关系是( )
| A、相交且过圆心 | B、相交但不过圆心 |
| C、相切 | D、相离 |
已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=log2x,则f(-
)=( )
| 5 |
| 2 |
| A、0 | ||
B、
| ||
| C、1 | ||
D、
|
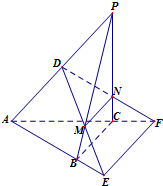 如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.
如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F. 函数f(x)=Asin(2x+φ),(A>0,|φ|<
函数f(x)=Asin(2x+φ),(A>0,|φ|<