题目内容
若a=(-2)-4，b=log23，c=(-3)3，则（ ）
| A、a＞b＞c |
| B、b＞a＞c |
| C、a＞c＞b |
| D、b＞c＞a |
考点：不等关系与不等式
专题：函数的性质及应用
分析：根据指数幂的性质和对数的取值范围即可比较大小．
解答：
解：a=（-2）-4=2-4=
∈(0，1)，b=log23＞1，c=（-3）3=-33＜0，
∴b＞a＞c，
故选：B．
| 1 |
| 16 |
∴b＞a＞c，
故选：B．
点评：本题主要考查指数幂和对数的大小比较，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
某家公司每月生产两种布料A和B，所有原料是两种不同颜色的羊毛，下表给出了生产每匹每种布料所需的羊毛量，以及可供使用的每种颜色的羊毛的总量．
已知生产每匹布料A、B的利润分别为120元、80元．那么公司每月应怎么安排生产两种布料A和B的匹数，才能够产生最大的利润，最大利润为（ ）元．
| 羊毛颜色 | 每匹需要 （ kg） | 供应量（kg） | |
| 布料A | 布料B | ||
| 红 | 4 | 4 | 1400 |
| 绿 | 6 | 3 | 1800 |
| A、38000 |
| B、32000 |
| C、28000 |
| D、48000 |
设数列{an}的前n项和为Sn，令Tn=
，称Tn为数列a1，a2，…，an的“理想数”，已知数列a1，a2，…，a502的“理想数”为2012，那么数列3，a1，a2，…，a502的“理想数”为（ ）
| S1+S2+…+Sn |
| n |
| A、2011 | B、2012 |
| C、2013 | D、2014 |
某几何体的三视图如所示，该几何体的体积为（ ）| A、20 | ||
B、
| ||
| C、56 | ||
| D、60 |
在区间[0，1]上任取两个数a，b，则函数f（x）=x2+ax+b2无零点的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
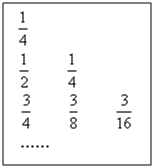如图给出一个“直角三角形数阵”：满足每一列成等差数列；从第三行起，每一行的数成等比数列，且每一行的公比相等，记第i行第j列的数为aij(i≥j，i，j∈N+)，则a86=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
三个数0.993.3，log3π，log20.8的大小关系为（ ）
| A、log3π＜0.993.3＜log20.8 |
| B、log20.8＜log3π＜0.993.3 |
| C、log20.8＜0.993.3＜log3π |
| D、0.993.3＜log20.8 l＜log3π |