题目内容
由于空气污染严重,某工厂生产了两种供人们外出时便于携带的呼吸装置,其质量按测试指标划分:指标大于等于88为优质产品.现随机抽取这两种装至各100件进行检测,检测结果统计如下:
(Ⅰ)试分别估计装置甲、装置乙为优质品的概率;
(Ⅱ)设该厂生产一件产品的利润率y与其质量指标t的关系式为y=
,根据以上统计数据,估计生产一件装置乙的利润率大于0的概率,若投资100万生产装置乙,请估计该厂获得的平均利润;
(Ⅲ)若投资100万,生产装置甲或装置乙中的一种,请分析生产那种装置获得利润的数学期望较大.
| 测试指标分组 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] | |
| 频 数 |
装置甲 | 8 | 12 | 40 | 32 | 8 |
| 装置乙 | 7 | 18 | 40 | 29 | 6 | |
(Ⅱ)设该厂生产一件产品的利润率y与其质量指标t的关系式为y=
|
(Ⅲ)若投资100万,生产装置甲或装置乙中的一种,请分析生产那种装置获得利润的数学期望较大.
考点:离散型随机变量的期望与方差
专题:综合题,概率与统计
分析:(I)根据频数,求比值,得到估计装置甲、装置乙为优质品的概率;
(II)根据题意得到变量对应的数字,结合变量对应的事件写出变量对应的概率,可得数据的期望值;
(Ⅲ)比较生产装置甲或装置乙的期望值,即可得出结论.
(II)根据题意得到变量对应的数字,结合变量对应的事件写出变量对应的概率,可得数据的期望值;
(Ⅲ)比较生产装置甲或装置乙的期望值,即可得出结论.
解答:
解:(Ⅰ)装置甲为优质品的概率
=0.4、装置乙为优质品的概率
=0.35;
(Ⅱ)设乙的利润率为ξ,则ξ的可能取值为-2,2,4,
P(ξ=-2)=0.07,P(ξ=2)=0.58,P(ξ=4)=0.35,
∴生产一件装置乙的利润率大于0的概率为P(ξ>0)=P(ξ=2)+P(ξ=4)=0.58+0.35=0.93,
Eξ=-2×0.07+2×0.58+4×0.35=2.42,
∴投资100万生产装置乙,估计该厂获得的平均利润为242万;
(Ⅲ)设甲的利润率为η,则η的可能取值为-2,2,4,
P(η=-2)=0.08,P(ξ=2)=0.52,P(ξ=4)=0.4,
∴Eη=-2×0.08+2×0.52+4×0.4=2.48,
∵Eη>Eξ,
∴生产甲种装置获得利润的数学期望较大.
| 32+8 |
| 100 |
| 29+6 |
| 100 |
(Ⅱ)设乙的利润率为ξ,则ξ的可能取值为-2,2,4,
P(ξ=-2)=0.07,P(ξ=2)=0.58,P(ξ=4)=0.35,
∴生产一件装置乙的利润率大于0的概率为P(ξ>0)=P(ξ=2)+P(ξ=4)=0.58+0.35=0.93,
Eξ=-2×0.07+2×0.58+4×0.35=2.42,
∴投资100万生产装置乙,估计该厂获得的平均利润为242万;
(Ⅲ)设甲的利润率为η,则η的可能取值为-2,2,4,
P(η=-2)=0.08,P(ξ=2)=0.52,P(ξ=4)=0.4,
∴Eη=-2×0.08+2×0.52+4×0.4=2.48,
∵Eη>Eξ,
∴生产甲种装置获得利润的数学期望较大.
点评:本题考查随机抽样和样本估计总体的实际应用,考查频数,频率和样本容量之间的关系,考查离散型随机变量的分布列和期望,本题是一个综合问题.

练习册系列答案
相关题目
过点A(2,b)和点B(3,-2)的直线的倾斜角为
,则b的值是( )
| 3π |
| 4 |
| A、-1 | B、1 | C、-5 | D、5 |
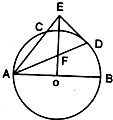 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.