题目内容
 已知正四面体的俯视图如图所示,其中ABCD是边长为2的正方形,则这个正四面体的体积为( )
已知正四面体的俯视图如图所示,其中ABCD是边长为2的正方形,则这个正四面体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:简单空间图形的三视图
专题:空间位置关系与距离
分析:根据题意,画出图形,结合题目所给数据,求出正四面体的棱长,可求其体积.
解答:
解:这个正四面体的位置是AC放在桌面上,
BD平行桌面,它的几何体如图,

正四面体的棱长就是俯视图正方形的对角线的长,
正四面体的棱长为:2
;
又∴当正四面体的棱长为a,它的体积为
a3.
∴所求正四面体的体积是:
×(2
)3=
.
故选:B
BD平行桌面,它的几何体如图,

正四面体的棱长就是俯视图正方形的对角线的长,
正四面体的棱长为:2
| 2 |
又∴当正四面体的棱长为a,它的体积为
| ||
| 12 |
∴所求正四面体的体积是:
| ||
| 12 |
| 2 |
| 8 |
| 3 |
故选:B
点评:本题考查由三视图求面积,正四面体的体积的求法,考查空间想象能力逻辑思维能力,是中档题.

练习册系列答案
相关题目
定义a⊕b=
,设函数f(x)=lnx⊕x,则f(2)+f(
)=( )
|
| 1 |
| 2 |
| A、4ln2 | B、-4ln2 |
| C、2 | D、0 |
下列不等式可以推出a>b的是( )
| A、ac>bc | ||||
B、
| ||||
| C、a+c>b+d | ||||
| D、a-c>b-c |
如果α在第二象限,则
必定在( )
| α |
| 2 |
| A、第一或第二象限 |
| B、第一或第三象限 |
| C、第三或第四象限 |
| D、第二或第四象限 |
设函数f(x)=|lnx|,则下列结论中正确的是( )
A、f(1)<f(
| ||
B、f(
| ||
C、f(e)<f(1)<f(
| ||
D、f(e)<f(
|
如图所示计算机程序的打印结果为( )
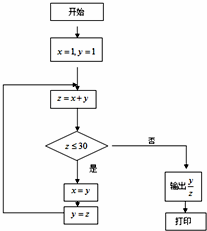

A、
| ||
B、
| ||
C、
| ||
D、
|
过点A(2,b)和点B(3,-2)的直线的倾斜角为
,则b的值是( )
| 3π |
| 4 |
| A、-1 | B、1 | C、-5 | D、5 |