题目内容
点P是椭圆
+
=1上的任意一点，F1、F2是椭圆的两个焦点，则△PF1F2面积的最大值为 ．
| x2 |
| 144 |
| y2 |
| 169 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由题意方程可知椭圆是焦点在y轴上的椭圆，求出焦距及短半轴长，代入三角形面积公式得答案．
解答：
解：由椭圆
+
=1，得a=12，b=13，
c2=a2-b2=25，c=5．
设P（x，y），
则S△PF1F2=
|F1F2||x|，
当|x|=12时，△PF1F2面积有最大值为
×10×12=60．
故答案为：60．
| x2 |
| 144 |
| y2 |
| 169 |
c2=a2-b2=25，c=5．
设P（x，y），
则S△PF1F2=
| 1 |
| 2 |
当|x|=12时，△PF1F2面积有最大值为
| 1 |
| 2 |
故答案为：60．
点评：本题考查了椭圆的简单几何性质，解答此题的关键是注意椭圆焦点在y轴上，是基础题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
设x，y满足约束条件
，若z=|
|的最小值为3，则a的值为（ ）
|
| x+2y+3 |
| x-1 |
| A、-1 | B、1 | C、-2 | D、2 |
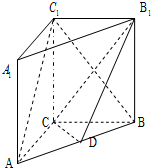如图，在三棱柱ABC-A1B1C1中，侧棱A1A垂直于底面ABC，AC=3，BC=4，AB=5，AA1=4点D是AB的中点，
已知函数f（x）=（2x+1）ln（2x+1）-a（2x+1）2-x（a＞0）．