题目内容
已知定义在R上的偶函数f(x)满足f(x-6)=f(x)+f(-3),则f(15)= .
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:定义在R上的偶函数f(x),则有f(-x)=f(x),由于f(x-6)=f(x)+f(-3),令x=3,求得f(-3)=0,
进而得到函数f(x)是最小正周期为6的周期函数,则f(15)=f(3),再由偶函数的定义,即可得到所求值.
进而得到函数f(x)是最小正周期为6的周期函数,则f(15)=f(3),再由偶函数的定义,即可得到所求值.
解答:
解:定义在R上的偶函数f(x),则有f(-x)=f(x),
由于f(x-6)=f(x)+f(-3),
即f(-3)=f(3)+f(-3)=2f(-3),
则f(-3)=0,
即有f(x-6)=f(x),即有f(x+6)=f(x),
函数f(x)是最小正周期为6的周期函数.
则f(15)=f(12+3)=f(3)=f(-3)=0,
故答案为:0.
由于f(x-6)=f(x)+f(-3),
即f(-3)=f(3)+f(-3)=2f(-3),
则f(-3)=0,
即有f(x-6)=f(x),即有f(x+6)=f(x),
函数f(x)是最小正周期为6的周期函数.
则f(15)=f(12+3)=f(3)=f(-3)=0,
故答案为:0.
点评:本题考查函数的奇偶性和周期性的运用:求函数值,考查运算能力,属于中档题.

练习册系列答案
相关题目
设x,y满足约束条件
,若z=|
|的最小值为3,则a的值为( )
|
| x+2y+3 |
| x-1 |
| A、-1 | B、1 | C、-2 | D、2 |
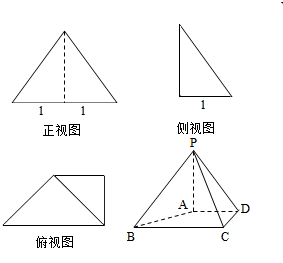 已知四棱锥P-ABCD的三视图如图所示,△PBC为正三角形.
已知四棱锥P-ABCD的三视图如图所示,△PBC为正三角形.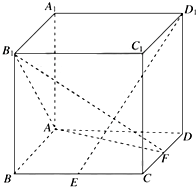 如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,点F是棱CD上的动点.
如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,点F是棱CD上的动点.