题目内容
6．一个几何体的三视图如图所示，则该几何体的体积等于（ ）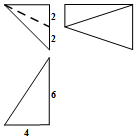
| A． | 16 | B． | 24 | C． | 48 | D． | 72 |
分析 如图所示，该几何体为四棱锥P-ABCD．其中底面ABCD是直角梯形，CD$\underset{∥}{=}$$\frac{1}{2}$AB，AB⊥AD，PA⊥底面ABCD．
解答 解：如图所示，该几何体为四棱锥P-ABCD．
其中底面ABCD是直角梯形，CD$\underset{∥}{=}$$\frac{1}{2}$AB，AB⊥AD，PA⊥底面ABCD．
∴该几何体的体积V=$\frac{1}{3}×PA×{S}_{梯形ABCD}$
=$\frac{1}{3}×$4×$\frac{2+4}{2}×6$=24．
故选：B．
点评 本题考查了四棱锥的三视图、体积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
16．如图，某几何体的三视图都是直角三角形，若几何体的最大棱长为2，则该几何体的外接球的体积是（ ）
| A． | $\sqrt{6}π$ | B． | $\frac{4}{3}π$ | C． | 4π | D． | 6π |
11．“a＜1，b=-4”是“圆x2+y2-2x+6y+5a=0关于直线y=x+b对称”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
18．已知函数f（x）=sinx-cosx，把f（x）的图象左移$\frac{π}{4}$个单位，得到g（x）的图象，则g（x）的解析式为（ ）
| A． | g（x）=$\sqrt{2}$sinx | B． | g（x）=-$\sqrt{2}$sinx | C． | g（x）=$\sqrt{2}$cosx | D． | g（x）=-$\sqrt{2}$cosx |