题目内容
15．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}（x+1），x＞0}\\{2f（x+4），x≤0}\end{array}\right.$，则f（-2）=2．分析 利用函数的性质求出f（-2）=2f（2），由此能求出结果．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}（x+1），x＞0}\\{2f（x+4），x≤0}\end{array}\right.$，
∴f（-2）=2f（2）=2log33=2．
故答案为：2．
点评 本题考查函数值的求法，涉及到函数的周期性、对数函数的性质及运算法则等基础知识，考查推理论证能力、运算求解能力，考查函数与方程思想，是基础题．
练习册系列答案
相关题目
5．
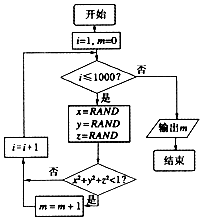我们可以用随机模拟的方法估计π的值，如图程序框图表示其基本步骤（函数RAND是产生随机数的函数，它能随机产生（0，1）内的任何一个实数）．若输出的结果为527，则由此可估计π的近似值为（ ）
我们可以用随机模拟的方法估计π的值，如图程序框图表示其基本步骤（函数RAND是产生随机数的函数，它能随机产生（0，1）内的任何一个实数）．若输出的结果为527，则由此可估计π的近似值为（ ）| A． | 3.126 | B． | 3.132 | C． | 3.151 | D． | 3.162 |
6．一个几何体的三视图如图所示，则该几何体的体积等于（ ）
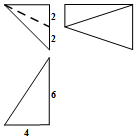
| A． | 16 | B． | 24 | C． | 48 | D． | 72 |
10．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}（x+1），x＞0}\\{2f（x+10），x≤0}\end{array}\right.$，则f（-2）等于（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
20．
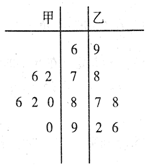甲、乙两名学生的六次数学测试成绩（百分制）如图所示．
①甲同学成绩的中位数大于乙同学成绩的中位数；
②甲同学的平均分比乙同学高；
③甲同学的平均分比乙同学低；
④甲同学成绩的标准差小于乙同学成绩的标准差．
上面说法正确的是（ ）
甲、乙两名学生的六次数学测试成绩（百分制）如图所示．①甲同学成绩的中位数大于乙同学成绩的中位数；
②甲同学的平均分比乙同学高；
③甲同学的平均分比乙同学低；
④甲同学成绩的标准差小于乙同学成绩的标准差．
上面说法正确的是（ ）
| A． | ③④ | B． | ①② | C． | ②④ | D． | ①③④ |
7．母线长为1的圆锥的侧面展开图的圆心角为$\frac{4}{3}$π，则该圆锥的体积是（ ）
| A． | $\frac{2\sqrt{5}}{81}$π | B． | $\frac{4\sqrt{5}}{27}$π | C． | $\frac{4\sqrt{5}}{81}$π | D． | $\frac{\sqrt{10}}{81}$π |
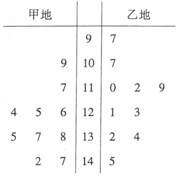在一次期末模拟测试中，某市教研室在甲、乙两地各抽取了10名学生的数学成绩，得到茎叶图如图所示．