题目内容

11．“a＜1，b=-4”是“圆x2+y2-2x+6y+5a=0关于直线y=x+b对称”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件

分析 根据圆的对称性结合充分条件和必要条件的定义进行判断即可．

解答 解：因为圆x2+y2-2x+6y+5a=0关于直线y=x+b对称，所以圆心（1，-3）在直线y=x+b上，所以-3=1+b，所以b=-4，
由圆x2+y2-2x+6y+5a=0得4+36-20a＞0，
所以a＜2，
所以充要条件是a＜2，b=-4，易知选A，
故选：A．

点评 本题主要考查充分条件和必要条件的判断，结合圆的对称性是解决本题的关键．

练习册系列答案
相关题目
1．P（x，y）是曲线$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}$（0≤θ＜π，θ是参数）上的动点，则$\frac{y}{x}$的取值范围是（　　）
A．[-$\frac{\sqrt{3}}{3}$，0]B．[-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$]C．[0，$\frac{\sqrt{3}}{3}$]D．（-∞，$\frac{\sqrt{3}}{3}$]
2．定义在R上的函数f（x）的导函数为f′（x），f（0）=0．若对任意x∈R，都有f（x）＞f′（x）+1，则使得f（x）+ex＜1成立的x的取值范围为（　　）
A．（-∞，0）B．（-∞，1）C．（-1，+∞）D．（0，+∞）
19．在△ABC中，内角A，B，C所对的边分别为a，b，c，且（2b-c）cosA=acosC，
（1）求A；
（2）若a=2$\sqrt{3}$，求△ABC的BC边上高的最大值．
6．一个几何体的三视图如图所示，则该几何体的体积等于（　　）
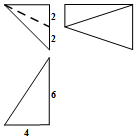
A．16B．24C．48D．72
16．已知正项数列{an}满足a1=1，且an+1=$\frac{a_n}{{2{a_n}+1}}（n∈{N^*}）$．
（1）证明数列$\{\frac{1}{a_n}\}$为等差数列，并求数列{an}的通项公式；
（2）设bn=（-1）n•n•an•an+1，求数列{bn}的前n项和Tn．
3．已知实数x、y满足条件$\left\{\begin{array}{l}{x≤2}\\{y≤2}\\{x+y-2≥0}\end{array}\right.$，则$\frac{y+1}{x+4}$的取值范围为[$\frac{1}{6}$，$\frac{3}{4}$]．
20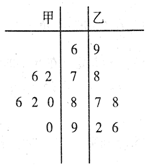．甲、乙两名学生的六次数学测试成绩（百分制）如图所示．
①甲同学成绩的中位数大于乙同学成绩的中位数；
②甲同学的平均分比乙同学高；
③甲同学的平均分比乙同学低；
④甲同学成绩的标准差小于乙同学成绩的标准差．
上面说法正确的是（　　）
A．③④B．①②C．②④D．①③④
1．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一条渐近线方程为$y=\frac{3}{4}x$，则双曲线的离心率为（　　）
A．$\frac{5}{3}$B．$\frac{{\sqrt{21}}}{3}$C．$\frac{5}{4}$D．$\frac{{\sqrt{7}}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网