题目内容

18．已知函数f（x）=sinx-cosx，把f（x）的图象左移$\frac{π}{4}$个单位，得到g（x）的图象，则g（x）的解析式为（　　）
A．g（x）=$\sqrt{2}$sinxB．g（x）=-$\sqrt{2}$sinxC．g（x）=$\sqrt{2}$cosxD．g（x）=-$\sqrt{2}$cosx

分析 利用两角差的正弦公式化简函数的解析式，再利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．

解答 解：把函数f（x）=sinx-cosx=$\sqrt{2}$sin（x-$\frac{π}{4}$）的图象左移$\frac{π}{4}$个单位，得到g（x）=$\sqrt{2}$sinx的图象，
故选：A．

点评 本题主要考查两角差的正弦公式，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．

练习册系列答案
相关题目
8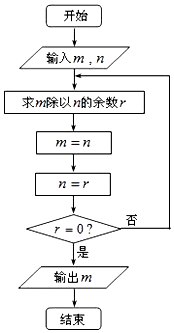．如图所示的程序框图描述的算法称为“欧几里得”辗转相除法，若输入m=2821，n=2015，则输出的m的值为（　　）
A．1B．403C．806D．2015
9．已知数列{an}中，点（an，an+1）在直线y=x+2上，首项a1=1．数列{an}的通项公式为an=2n-1．
6．一个几何体的三视图如图所示，则该几何体的体积等于（　　）
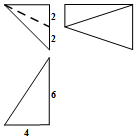
A．16B．24C．48D．72
13．已知向量$\overrightarrow a，\overrightarrow b$满足$|{\overrightarrow a}|=2$，$|\overrightarrow b|=2$，$（\overrightarrow a+\overrightarrow b）•（3\overrightarrow a-\overrightarrow b）=4$，则$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{2π}{3}$．
3．已知实数x、y满足条件$\left\{\begin{array}{l}{x≤2}\\{y≤2}\\{x+y-2≥0}\end{array}\right.$，则$\frac{y+1}{x+4}$的取值范围为[$\frac{1}{6}$，$\frac{3}{4}$]．
10．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}（x+1），x＞0}\\{2f（x+10），x≤0}\end{array}\right.$，则f（-2）等于（　　）
A．1B．2C．3D．4
7．母线长为1的圆锥的侧面展开图的圆心角为$\frac{4}{3}$π，则该圆锥的体积是（　　）
A．$\frac{2\sqrt{5}}{81}$πB．$\frac{4\sqrt{5}}{27}$πC．$\frac{4\sqrt{5}}{81}$πD．$\frac{\sqrt{10}}{81}$π
8．把复数z的共轭复数记作$\overline{z}$，若（1+i）z=1-i，i为虚数单位，则$\overline{z}$=（　　）
A．iB．-iC．1-iD．1+i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网