题目内容

16．如图，某几何体的三视图都是直角三角形，若几何体的最大棱长为2，则该几何体的外接球的体积是（　　）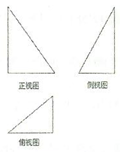
A．$\sqrt{6}π$B．$\frac{4}{3}π$C．4πD．6π

分析 由三视图可知：该几何体为三棱锥P-ABC，其中PA⊥底面ABC，AC⊥BC．则该几何体的最大棱长为PB，为外接球的直径．

解答 解：由三视图可知：该几何体为三棱锥P-ABC，其中PA⊥底面ABC，AC⊥BC．
则该几何体的最大棱长为PB=2，为外接球的直径．
∴该几何体的外接球的体积V=$\frac{4π×{1}^{3}}{3}$=$\frac{4π}{3}$．
故选：B．

点评 本题考查了三棱锥的三视图、球体积计算公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
6．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{b}$|=3，|$\overrightarrow{a}$|=2|$\overrightarrow{b}-\overrightarrow{a}$|，若|$\overrightarrow{a}$+λ$\overrightarrow{b}$|≥3恒成立，则实数λ的取值范围为（-∞，-3]∪[$\frac{1}{3}$，+∞）．
7．执行如图所示的程序框图，输入的S0值为10时，则输出的S的值为（　　）
A．-4B．2C．-20D．6
4．在△ABC中，a=2，b=3，C=120°，求边c的大小及△ABC的面积．
11．有限与无限转化是数学中一种重要思想方法，如在《九章算术》方田章圆田术（刘徽注）中：“割之又割以至于不可割，则与圆合体而无所失矣．”说明“割圆术”是一种无限与有限的转化过程，再如$\sqrt{2+\sqrt{2+\sqrt{2+…}}}$中“…”即代表无限次重复，但原式却是个定值x．这可以通过方程$\sqrt{2+x}$=x确定出来x=2，类似地可以把循环小数化为分数，把0.$\stackrel{•}{3}\stackrel{•}{6}$化为分数的结果为$\frac{4}{11}$．
1．P（x，y）是曲线$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}$（0≤θ＜π，θ是参数）上的动点，则$\frac{y}{x}$的取值范围是（　　）
A．[-$\frac{\sqrt{3}}{3}$，0]B．[-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$]C．[0，$\frac{\sqrt{3}}{3}$]D．（-∞，$\frac{\sqrt{3}}{3}$]
8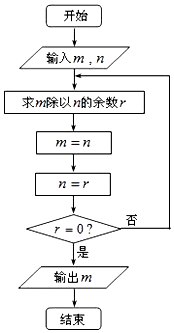．如图所示的程序框图描述的算法称为“欧几里得”辗转相除法，若输入m=2821，n=2015，则输出的m的值为（　　）
A．1B．403C．806D．2015
5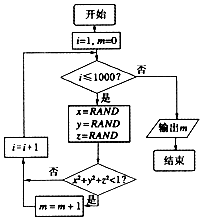．我们可以用随机模拟的方法估计π的值，如图程序框图表示其基本步骤（函数RAND是产生随机数的函数，它能随机产生（0，1）内的任何一个实数）．若输出的结果为527，则由此可估计π的近似值为（　　）
A．3.126B．3.132C．3.151D．3.162
6．一个几何体的三视图如图所示，则该几何体的体积等于（　　）
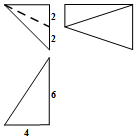
A．16B．24C．48D．72

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网