Question

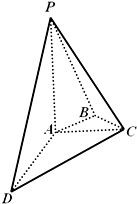如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1．
（1）证明：PC⊥AD；
（2）求二面角A-PC-D的正弦值（理科）；
（2）求直线PB与平面PAC所成角的正弦值（文科）；
（3）设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长．

Answer 1

考点：二面角的平面角及求法,异面直线及其所成的角

专题：空间位置关系与距离,空间角

分析：（1）根据已知条件容易证明AD⊥平面PAC，所以得到PC⊥AD；
（2理）过A作AM⊥PC，垂足为M，连接DM，则 能够说明∠AMD便是二面角A-PC-D的平面角，并且△AMD是Rt△，所以根据已知的边的长度即可求出sin∠AMD=

AD

DM

；
（2文）取AC中点N，连接BN，PN，则BN⊥平面PAC，所以∠BPN是直线PB与平面PAC所成角，根据已知的边长即可求出sin∠BPN=

BN

PB

；
（3）先找到异面直线BE，CD所成角：过B作BF∥CD，交AD于F，连接BE，EF，则∠EBF或其补角为异面直线BE，CD所成角．能够求出sin∠AFB=

1

5

，sin∠FAB=

2

2

，AB=

2

2

，所以在△ABF中由正弦定理可求出BF=

5

2

，而由余弦定理可求得AF=

1

2

．设AE=h，可表示出EF，EB，并且可比较出EF＜EB，所以∠EBF=30°，由余弦定理即可求得AE的长．

解答： 解：（1）∵PA⊥平面ABCD，AD?平面ABCD；
∴PA⊥AD，即AD⊥PA；
又AD⊥AC，PA∩AC=A；
∴AD⊥平面PAC，PC?平面PAC；
∴AD⊥PC，即PC⊥AD；
（2理）如图，过A作AM⊥PC，交PC于M，并连接DM；
由（1）知PC⊥AD，∴PC⊥平面ADM，DM?平面ADM；
∴PC⊥DM；
∴∠AMD是二面角A-PC-D的平面角；
PC=

5

；
∴

5

•AM=1•2；
∴AM=

2

5

；
∴在Rt△ADM中，DM=

4+ 4 5

=

24 5

，sin∠AMD=

AD

DM

=

2

24 5

=

30

6

；
（2文）取AC中点N，连接PN，由已知条件知，AB=BC=

2

2

，
∴BN⊥AC；
∵PA⊥平面ABCD；
∴PA⊥BN，即BN⊥PA，PA∩AC=A；
∴BN⊥平面PAC；
∴∠BPN是直线PB与平面PAC所成角；
BN=

2

2

•

2

2

=

1

2

；
在Rt△PAB中，PB=

4+ 1 2

=

3

2

；
∴在Rt△PBN中，sin∠BPN=

BN

PB

=

1 2

3 2

=

2

6

；
（3）如图，因为∠ADC＜45°，故过点B作CD的平行线必与线段AD相交，设交点为F，连接BE，EF；
∴∠EBF或其补角为异面直线BE与CD所成的角；
由于BF∥CD，故∠AFB=∠ADC；
在Rt△DAC中，CD=

5

，sin∠ADC=

1

5

；
∴sin∠AFB=

1

5

；
∴在△AFB中，由

BF

sin∠FAB

=

AB

sin∠AFB

，AB=

2

2

，sin∠FAB=sin135°=

2

2

可得：BF=

5

2

；
由余弦定理，BF²=AB²+AF²-2AB•AF•cos∠FAB可得，

5

4

=

1

2

+AF2+AF，
解得：AF=

1

2

，设AE=h；
在Rt△EAF中，EF=

1 4 +h2

；
在Rt△EAB中BE=

1 2 +h2

；
∴在△EBF中，EF＜BE，∴∠EBF=30°；
∴由余弦定理得：
cos30°=

BE2+BF2-EF2

2BE•BF

=

1 2 +h2+ 5 4 - 1 4 -h2

2 1 2 +h2 • 5 2

=

3

2

；
解得h=

10

10

；
∴AE=

10

10

．

点评：考查线面垂直的性质，线面垂直的判定定理，以及二面角的平面角的概念及找法，线面角的概念及找法，异面直线所成角的概念及找法，以及正弦定理，余弦定理的运用．