题目内容
1.已知数列${a_n}=n•sin\frac{nπ}{2}$,则a1+a2+a3+…+a100=( )| A. | -48 | B. | -50 | C. | -52 | D. | -49 |
分析 通过计算前几项可知a4n-3+a4n-2+a4n-3+a4n=-2,进而计算可得结论.
解答 解:∵${a_n}=n•sin\frac{nπ}{2}$,
∴a1=1,a2=0,a3=-3,a4=0,a5=5,a6=0,a7=-7,a8=0,…
∴a4n-3+a4n-2+a4n-1+a4n=-2,
∴a1+a2+a3+…+a100=-2×25=-50,
故选:B.
点评 本题考查数列的通项及前n项和,找出规律是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.设α、β为两个不同平面,若直线l在平面α内,则“α⊥β”是“l⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.若a,b∈R,且ab>0,则“a=b”是“$\frac{b}{a}+\frac{a}{b}≥2$等号成立”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既非充分又非必要条件 |
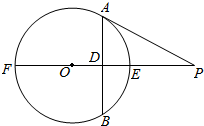 如图,已知PA为⊙O的切线,A为切点,直线PO交⊙O于点E、F,过点A作PO的垂线交⊙O于点B,垂足为D.
如图,已知PA为⊙O的切线,A为切点,直线PO交⊙O于点E、F,过点A作PO的垂线交⊙O于点B,垂足为D.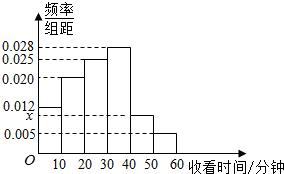 某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].则图中x的值为0.01.
某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].则图中x的值为0.01.