题目内容
16.数列{an}是等差数列,a2和a2014是方程5x2-6x+1=0的两根,则数列{an}的前2015项的和为1209.分析 利用韦达定理可知a2+a2014=$\frac{6}{5}$,进而通过等差数列中“下标和相等两项和相等”及求和公式计算即得结论.
解答 解:∵a2和a2014是方程5x2-6x+1=0的两根,
∴a2+a2014=$\frac{6}{5}$,
又∵数列{an}是等差数列,
∴数列{an}的前2015项的和为$\frac{2015({a}_{2}+{a}_{2014})}{2}$=$\frac{2015}{2}$•$\frac{6}{5}$=1209,
故答案为:1209.
点评 本题考查数列的通项及前n项和,利用等差数列中“下标和相等两项和相等”是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
1.已知数列${a_n}=n•sin\frac{nπ}{2}$,则a1+a2+a3+…+a100=( )
| A. | -48 | B. | -50 | C. | -52 | D. | -49 |
5.已知函数f(x)=ex+3,则f(x)在x=0处切线的方程是( )
| A. | x-y+4=0 | B. | x+y-4=0 | C. | 4x-y+4=0 | D. | 4x+y-4=0 |
6.已知i是虚数单位,则复数i(1+i)的共轭复数为( )
| A. | 1+i | B. | l-i | C. | -l+i | D. | -l-i |
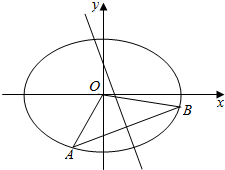 已知椭圆$\frac{{x}^{2}}{2}$+y2=1上两个不同的点A,B关于直线$y=mx+\frac{1}{2}(m≠0)$对称.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1上两个不同的点A,B关于直线$y=mx+\frac{1}{2}(m≠0)$对称.