题目内容
6.已知函数y=f(x)是单调递增函数,其反函数是y=f-1(x).(1)若y=x2-1(x>$\frac{1}{2}$),求y=f-1(x)并写出定义域M;
(2)对于(1)的y=f-1(x)和M,设任意x1∈M,x2∈M,x1≠x2,求证:|f-1(x1)-f-1(x2)|<|x1-x2|;
(3)求证:若y=f(x)和y=f-1(x)有交点,那么交点一定在y=x上.
分析 (1)由$y={x^2}-1({x>\frac{1}{2}})$,解得x=$\sqrt{y+1}$,把x与y互换,即可得出y=f-1(x);
(2)任意取x1∈M,x2∈M,x1≠x2,则$|{{f^{-1}}({x_1})-{f^{-1}}({x_2})}|=|{\sqrt{{x_1}+1}-\sqrt{{x_2}+1}}|=\frac{{|{{x_1}-{x_2}}|}}{{\sqrt{{x_1}+1}+\sqrt{{x_2}+1}}}$,利用不等式的性质即可证明;
(3)设(a,b)是y=f(x)和y=f-1(x)的交点,即$\left\{\begin{array}{l}b=f(a)\\ b={f^{-1}}(a)\end{array}\right.$,可得a=f(b),b=f(a),对a与b的大小关系分类讨论,再利用反函数的性质即可证明.
解答 (1)解:由$y={x^2}-1({x>\frac{1}{2}})$,解得x=$\sqrt{y+1}$,把x与y互换,可得y=f-1(x)=$\sqrt{x+1}$,x$>-\frac{3}{4}$,M=$(-\frac{3}{4},+∞)$.
(2)证明:任意取x1∈M,x2∈M,x1≠x2,则$|{{f^{-1}}({x_1})-{f^{-1}}({x_2})}|=|{\sqrt{{x_1}+1}-\sqrt{{x_2}+1}}|=\frac{{|{{x_1}-{x_2}}|}}{{\sqrt{{x_1}+1}+\sqrt{{x_2}+1}}}$,
∵${x_1}>-\frac{3}{4}$,∴$\sqrt{{x_1}+1}>\frac{1}{2}$,${x_2}>-\frac{3}{4}$,∴$\sqrt{{x_2}+1}>\frac{1}{2}$,∴$\sqrt{{x_1}+1}+\sqrt{{x_2}+1}>1$,∴$0<\frac{1}{{\sqrt{{x_1}+1}+\sqrt{{x_2}+1}}}<1$,
∴$\frac{{|{{x_1}-{x_2}}|}}{{\sqrt{{x_1}+1}+\sqrt{{x_2}+1}}}<|{{x_1}-{x_2}}|$,∴$|{{f^{-1}}({x_1})-{f^{-1}}({x_2})}|<|{{x_1}-{x_2}}|$.
(3)证明:设(a,b)是y=f(x)和y=f-1(x)的交点,
即$\left\{\begin{array}{l}b=f(a)\\ b={f^{-1}}(a)\end{array}\right.$,∴a=f(b),b=f(a),
当a=b,显然在y=x上;
当a>b,函数y=f(x)是单调递增函数,∴f(a)>f(b),∴b>a矛盾;
当a<b,函数y=f(x)是单调递增函数,∴f(a)<f(b),∴b<a矛盾;
因此,若y=f(x)和y=f-1(x)的交点一定在y=x上.
点评 本题考查了反函数的求法及其性质、函数的单调性,考查了推理能力与计算能力,属于中档题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案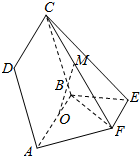 如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1(Ⅰ)设FC的中点为M,求证:OM∥面DAF;
(Ⅱ)求证:AF⊥面CBF.
| A. | -48 | B. | -50 | C. | -52 | D. | -49 |
| A. | ϕ | B. | {2} | C. | {0} | D. | {-2} |