题目内容
已知函数f(x)=xsinx+cosx,给出如命题:
①f(x)是偶函数;
②f(x)在[0,
]上单调递减,在(
,2π]上单调递增;
③函数f(x)在[-
,
]上有3个零点;
④当x≥0时,f(x)≤x2+1恒成立;
其中正确的命题序号是 .
①f(x)是偶函数;
②f(x)在[0,
| 3π |
| 2 |
| 3π |
| 2 |
③函数f(x)在[-
| 3π |
| 2 |
| 3π |
| 2 |
④当x≥0时,f(x)≤x2+1恒成立;
其中正确的命题序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用偶函数的定义判断;
②利用导数求解,导数大于0求增区间,导数小于0求减区间;
③研究极值、端点处的函数值的符号;
④转化为f(x)-(x2+1)≤0恒成立,因此只需求左边函数的最大值小于0即可.
②利用导数求解,导数大于0求增区间,导数小于0求减区间;
③研究极值、端点处的函数值的符号;
④转化为f(x)-(x2+1)≤0恒成立,因此只需求左边函数的最大值小于0即可.
解答:
解:对于①,显然定义域为R,f(-x)=-xsin(-x)+cos(-x)=xsinx+cosx=f(x).所以函数为偶函数,所以①为真命题;
对于②,f′(x)=sinx+xcosx-sinx=xcosx,当x∈[0,
]时,f′(x)>0,此时函数为增函数,故②为假命题;
对于③,令f(x)=0,所以
=-tanx,做出y=
及y=-tanx在[-
,
]上的图象可知,它们在[-
,
]上只有两个交点,所以原函数在[-
,
]有两个零点,故③为假命题;

对于④,要使当x≥0时,f(x)≤x2+1恒成立,只需当x≥0时,f(x)-x2-1≤0恒成立,即y=xsinx+cosx-x2-1≤0恒成立,而y′=xcosx-2x=(cosx-2)x显然小于等于0恒成立,所以该函数在[0,+∞)上递减,因此x=0时ymax=0+cos0-1=0,故当x≥0时,f(x)≤x2+1恒成立,故④为真命题.
故答案为①④.
对于②,f′(x)=sinx+xcosx-sinx=xcosx,当x∈[0,
| π |
| 2 |
对于③,令f(x)=0,所以
| 1 |
| x |
| 1 |
| x |
| 3π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |

对于④,要使当x≥0时,f(x)≤x2+1恒成立,只需当x≥0时,f(x)-x2-1≤0恒成立,即y=xsinx+cosx-x2-1≤0恒成立,而y′=xcosx-2x=(cosx-2)x显然小于等于0恒成立,所以该函数在[0,+∞)上递减,因此x=0时ymax=0+cos0-1=0,故当x≥0时,f(x)≤x2+1恒成立,故④为真命题.
故答案为①④.
点评:本题考查了利用导数研究函数的单调性、最值、零点的方法,要注意数形结合的思想的应用.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
在空间中,下列命题正确的是( )
| A、三条直线两两相交,则这三条直线确定一个平面 |
| B、若平面α⊥β,且α∩β=l,则过α内一点P与l垂直的直线垂直于平面β |
| C、若直线m与平面α内的一条直线平行,则m∥α |
| D、若直线a与直线b平行,且直线l⊥a,则l∥b |
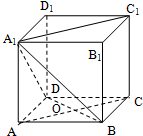 如图,在棱长为a的正方体 ABCD-A1B1C1D1 中,AC 与BD相交于点O.
如图,在棱长为a的正方体 ABCD-A1B1C1D1 中,AC 与BD相交于点O.