题目内容
过抛物线y2=2px(p>0)的焦点F作倾斜角为30°的直线交抛物线于A、B两点,若线段AB的长为8,则p= .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:抛物线的方程可求得焦点坐标,进而根据斜率表示出直线的方程,与抛物线的方程联立消去y,进而根据韦达定理表示出x1+x2和x1x2,进而利用配方法求得|x1-x2|,利用弦长公式表示出段AB的长求得p.
解答:
解:由题意可知过焦点的倾斜角为30°直线方程为y=
(x-
),
联立
可得:⇒x2-7px+
=0,
∴x1+x2=7p,x1x2=
,
∴|x1-x2|=
=
=4
p,
∴|AB|=
|x1-x2|=
×4
p=8,
解得:p=1,
故答案为:1
| ||
| 3 |
| p |
| 2 |
联立
|
| p2 |
| 4 |
∴x1+x2=7p,x1x2=
| p2 |
| 4 |
∴|x1-x2|=
| (x1+x2)2-4x1x2 |
(7p)2-4×
|
| 3 |
∴|AB|=
1+(
|
2
| ||
| 3 |
| 3 |
解得:p=1,
故答案为:1
点评:本题主要考查了抛物线的简单性质.涉及直线与抛物线的关系时,往往是利用韦达定理设而不求.

练习册系列答案
相关题目
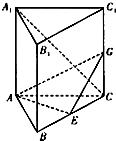 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.