题目内容
已知函数f(x)=(x2+ax+b)ex在点(0,f(0))处的切线方程是y=-2x+1,其中e是自然对数的底数.
(Ⅰ) 求实数a、b的值;
(Ⅱ) 求函数f(x)的极值.
(Ⅰ) 求实数a、b的值;
(Ⅱ) 求函数f(x)的极值.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:函数的性质及应用,导数的综合应用
分析:(Ⅰ) 由f(x)=(x2+ax+b)ex,得f'(x)=[x2+(a+2)x+a+b]ex,因为函数f(x)在点(0,f(0))处的切线方程是y=-2x+1,故(0,f(0))适合方程y=-2x+1,且f′(0)=-2;联立可得结果.
(Ⅱ)由(Ⅰ)知f(x)=(x2-3x+1)ex,f'(x)=(x2-x-2)ex=(x+1)(x-2)ex,令f'(x)=0,得x1=-1或x2=2.再判断这两点左右导数的符号,求出极值.
(Ⅱ)由(Ⅰ)知f(x)=(x2-3x+1)ex,f'(x)=(x2-x-2)ex=(x+1)(x-2)ex,令f'(x)=0,得x1=-1或x2=2.再判断这两点左右导数的符号,求出极值.
解答:
(Ⅰ) 由f(x)=(x2+ax+b)ex,得f'(x)=[x2+(a+2)x+a+b]ex,
因为函数f(x)在点(0,f(0))处的切线方程是y=-2x+1,
所以
即
解得a=-3,b=1.
(Ⅱ)由(Ⅰ)知f(x)=(x2-3x+1)ex,f'(x)=(x2-x-2)ex=(x+1)(x-2)ex,
令f'(x)=0,得x1=-1或x2=2.
当x<-1时,f'(x)>0,函数f(x)单调递增;当-1<x<2时,f'(x)<0,函数f(x)单调递减;当x>2时,f'(x)>0,函数f(x)单调递增,
故当x=-1时,函数f(x)取得极大值,f(x)极大值=f(-1)=
;当x=2时,函数f(x)取得极小值,f(x)极小值=f(2)=-e2.
因为函数f(x)在点(0,f(0))处的切线方程是y=-2x+1,
所以
|
|
解得a=-3,b=1.
(Ⅱ)由(Ⅰ)知f(x)=(x2-3x+1)ex,f'(x)=(x2-x-2)ex=(x+1)(x-2)ex,
令f'(x)=0,得x1=-1或x2=2.
当x<-1时,f'(x)>0,函数f(x)单调递增;当-1<x<2时,f'(x)<0,函数f(x)单调递减;当x>2时,f'(x)>0,函数f(x)单调递增,
故当x=-1时,函数f(x)取得极大值,f(x)极大值=f(-1)=
| 5 |
| e |
点评:本题主要考查函数与导数的关系,特别是曲线的切线与函数导数之间的关系,属于中档题.

练习册系列答案
相关题目
在空间中,下列命题正确的是( )
| A、三条直线两两相交,则这三条直线确定一个平面 |
| B、若平面α⊥β,且α∩β=l,则过α内一点P与l垂直的直线垂直于平面β |
| C、若直线m与平面α内的一条直线平行,则m∥α |
| D、若直线a与直线b平行,且直线l⊥a,则l∥b |
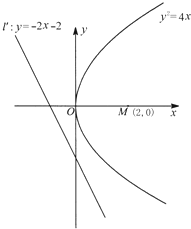 过点M(2,0)的直线l与抛物线C:y2=4x相交于A,B两点,过点A,B分别作y轴的垂线交直线l′:y=-2x-2于点A′,B′.
过点M(2,0)的直线l与抛物线C:y2=4x相交于A,B两点,过点A,B分别作y轴的垂线交直线l′:y=-2x-2于点A′,B′.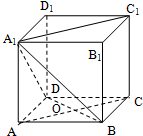 如图,在棱长为a的正方体 ABCD-A1B1C1D1 中,AC 与BD相交于点O.
如图,在棱长为a的正方体 ABCD-A1B1C1D1 中,AC 与BD相交于点O.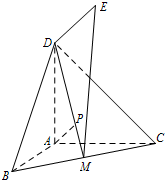 如图,DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.
如图,DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.