题目内容
 如图,已知正三棱柱ABC-A′B′C′棱长均为2,E为AB中点.点D在侧棱BB′上.
如图,已知正三棱柱ABC-A′B′C′棱长均为2,E为AB中点.点D在侧棱BB′上.(Ⅰ)求AD+DC′的最小值;
(Ⅱ)当AD+DC′取最小值时,在CC′上找一点F,使得EF∥面ADC′.
考点:直线与平面平行的判定,多面体和旋转体表面上的最短距离问题
专题:空间位置关系与距离
分析:(Ⅰ)将三棱柱的侧面展开,由题意知当D为BB′中点时,AD+DC′最小,由此能求出AD+DC′的最小值.
(Ⅱ)过点E作EM∥AD交BB′于M,M为BD中点,过点M作MF∥DC′交CC′于F,由面MEF∥面ADC′,得EF∥面ADC′.
(Ⅱ)过点E作EM∥AD交BB′于M,M为BD中点,过点M作MF∥DC′交CC′于F,由面MEF∥面ADC′,得EF∥面ADC′.
解答:
解:(Ⅰ)如图,将三棱柱的侧面展开,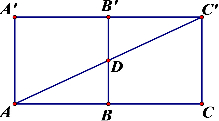
由题意知当D为BB′中点时,AD+DC′最小,
最小值为d=
=2
.(4分)
(Ⅱ)过点E作EM∥AD交BB′于M,所以M为BD中点,(6分)
过点M作MF∥DC′交CC′于F,
∴C′F=
,(10分)
∵EM∩MF=M,
∴面MEF∥面ADC′,∴EF∥面ADC′.(12分)

由题意知当D为BB′中点时,AD+DC′最小,
最小值为d=
| 42+22 |
| 5 |
(Ⅱ)过点E作EM∥AD交BB′于M,所以M为BD中点,(6分)
过点M作MF∥DC′交CC′于F,
∴C′F=
| 1 |
| 2 |
∵EM∩MF=M,
∴面MEF∥面ADC′,∴EF∥面ADC′.(12分)
点评:本题考查两线段和的最小值的求法,考查使直线与平面平行的点的位置的确定,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,在四面体P-ABC中,PA⊥平面ABC,AB=3,AC=4,BC=5,且D,E,F分别为BC,PC,AB的中点.
如图,在四面体P-ABC中,PA⊥平面ABC,AB=3,AC=4,BC=5,且D,E,F分别为BC,PC,AB的中点.