题目内容
 如图,在四面体P-ABC中,PA⊥平面ABC,AB=3,AC=4,BC=5,且D,E,F分别为BC,PC,AB的中点.
如图,在四面体P-ABC中,PA⊥平面ABC,AB=3,AC=4,BC=5,且D,E,F分别为BC,PC,AB的中点.(1)求证:AC⊥PB;
(2)在棱PA上是否存在一点G,使得FG∥平面ADE?证明你的结论.
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)由勾股定理得AC⊥AB,由线面垂直得PA⊥AC.从而AC⊥平面PAB.由此能证明AC⊥PB.
(2)取PA中点G时,FG∥平面ADE.由D、E分别是棱BC、PC的中点,得DE∥PB从而PB∥平面ADE,由FG∥PB,又FG?平面ADE,能证明FG∥平面ADE.
(2)取PA中点G时,FG∥平面ADE.由D、E分别是棱BC、PC的中点,得DE∥PB从而PB∥平面ADE,由FG∥PB,又FG?平面ADE,能证明FG∥平面ADE.
解答:
(1)证明:在△ABC中,AB=3,AC=4,BC=5,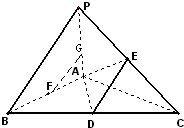
∴AB2+AC2=BC2
∴AC⊥AB,
又PA⊥平面ABC,AC?平面ABC,
∴PA⊥AC.又PA∩AB=A,
∴AC⊥平面PAB.
而PB?平面PAB,∴AC⊥PB.
(2)解:取PA中点G时,FG∥平面ADE.
证明如下:
∵D、E分别是棱BC、PC的中点,
∴DE∥PB. 又PB?平面ADE,DE?平面ADE
∴PB∥平面ADE,
在棱PA上取中点G,连结FG,
∵F是AB中点,
∴FG∥PB,又FG?平面ADE,
∴FG∥平面ADE.

∴AB2+AC2=BC2
∴AC⊥AB,
又PA⊥平面ABC,AC?平面ABC,
∴PA⊥AC.又PA∩AB=A,
∴AC⊥平面PAB.
而PB?平面PAB,∴AC⊥PB.
(2)解:取PA中点G时,FG∥平面ADE.
证明如下:
∵D、E分别是棱BC、PC的中点,
∴DE∥PB. 又PB?平面ADE,DE?平面ADE
∴PB∥平面ADE,
在棱PA上取中点G,连结FG,
∵F是AB中点,
∴FG∥PB,又FG?平面ADE,
∴FG∥平面ADE.
点评:本题考查异面直线垂直的证明,考查使直线与平面平行的点的位置的确定,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,已知正三棱柱ABC-A′B′C′棱长均为2,E为AB中点.点D在侧棱BB′上.
如图,已知正三棱柱ABC-A′B′C′棱长均为2,E为AB中点.点D在侧棱BB′上. 已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示.求:
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示.求: