题目内容
若存在实数x使|x-m|+|x+1|≤2成立，则实数m的取值范围是 ．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：根据绝对值的意义可得|x-m|+|x+1|的最小值为|m+1|，再由|m+1|≤2，求得实数m的取值范围．
解答：
解：根据绝对值得意义，|x-m|+|x+1|表示数轴上的x对应点到m、-1对应点的距离之和，
它的最小值为|m+1|．
由题意可得|m+1|≤2，即-2≤m+1≤2，解得-3≤m≤1，
故答案为：[-3，1]．
它的最小值为|m+1|．
由题意可得|m+1|≤2，即-2≤m+1≤2，解得-3≤m≤1，
故答案为：[-3，1]．
点评：本题主要考查绝对值的意义，绝对值不等式的解法，关键是去掉绝对值，属于基础题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
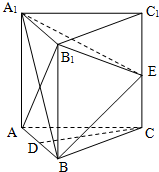如图，在三棱柱ABC-A1B1C1中，每个侧面均为边长为2的正方形，D为底边AB的中点，E为侧棱CC1的中点．
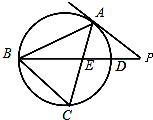如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交AC于点E，交⊙O于点D，若PE=PA，∠ABC=60°，PD=1，BD=8，则BC=