题目内容
已知集合A={x|x2+（p+2）x+1=0，x∈R}，且A⊆负实数，求实数p的取值范围．
考点：集合的包含关系判断及应用
专题：集合
分析：由A⊆负实数集，可知：A为空集，或者A满足：x2+（p+2）x+1=0有负根．
解答：
解：∵A⊆负实数集，∴A为空集，或者A中：x2+（p+2）x+1=0有负根．
若为空集：则△=（p+2）2-4＜0，解得-4＜p＜0．
若A中：x2+（p+2）x+1=0有负根．∵1＞0，∴△=（p+2）2-4≥0，且-（p+2）＜0，解得p≥0．
综上可得：实数p的取值范围是（-4，0）∪[0，+∞）．
若为空集：则△=（p+2）2-4＜0，解得-4＜p＜0．
若A中：x2+（p+2）x+1=0有负根．∵1＞0，∴△=（p+2）2-4≥0，且-（p+2）＜0，解得p≥0．
综上可得：实数p的取值范围是（-4，0）∪[0，+∞）．
点评：本题考查了集合之间的关系和分类讨论的思想方法，考查了推理能力，属于基础题．
练习册系列答案
相关题目
F1，F2是椭圆
+
=1（a＞b＞0）的左、右焦点，若在椭圆上存在点P，且满足|PF1|=2|PF2|，则椭圆的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||
B、（
| ||
C、（
| ||
D、（0，
|
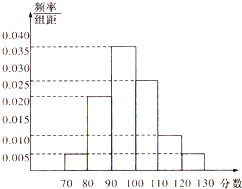我校高1201、1202、1203、1204四个班，从中随机抽取部分学生进行成绩统计，各班被抽取学生的人数恰好成等差数列，人数最少的班被抽取了24人，抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图，其中分数在[120，130]的人数为6人．
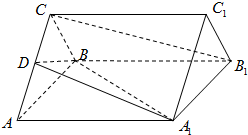如图，正三棱柱ABC-A1B1C1的底面边长是2，侧棱长是
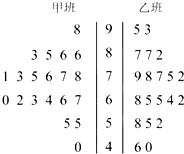某次月考从甲、乙两班中各抽取20个物理成绩，整理数据得到茎叶图如图所示，根据茎叶图解决下列问题．