题目内容
已知函数f(x)=ax2+
,其中a∈R.
(1)讨论函数f(x)的奇偶性,并证明你的结论;
(2)若函数f(x)在区间[1,+∞)上为增函数,求a的取值范围.
| 1 |
| x |
(1)讨论函数f(x)的奇偶性,并证明你的结论;
(2)若函数f(x)在区间[1,+∞)上为增函数,求a的取值范围.
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:综合题,函数的性质及应用
分析:(1)分a=0,a≠0两种情况讨论,利用奇偶性的定义可判断;
(2)函数f(x)在区间[1,+∞)上为增函数,等价于f′(x)≥0在[1,+∞)上恒成立,分离出参数化为函数的最值即可;
(2)函数f(x)在区间[1,+∞)上为增函数,等价于f′(x)≥0在[1,+∞)上恒成立,分离出参数化为函数的最值即可;
解答:
解:(1)当a=0时f(x)为奇函数;当a≠0时f(x)为非奇非偶函数.证明如下:
∵f(x)=ax2+
,
∴f(-x)=ax2-
,
当a=0时,f(-x)=-f(x)=-
,f(x)为奇函数;
当a≠0时,f(-x)≠f(x),且f(-x)≠-f(x),
此时f(x)为非奇非偶函数.
(2)f′(x)=2ax-
,
∵f(x)在区间[1,+∞)上为增函数,
∴f′(x)≥0在[1,+∞)上恒成立,即2a≥
在[1,+∞)上恒成立,
而
在在[1,+∞)上单调递减,∴
≤1,
∴2a≥1,解得a≥
.
∵f(x)=ax2+
| 1 |
| x |
∴f(-x)=ax2-
| 1 |
| x |
当a=0时,f(-x)=-f(x)=-
| 1 |
| x |
当a≠0时,f(-x)≠f(x),且f(-x)≠-f(x),
此时f(x)为非奇非偶函数.
(2)f′(x)=2ax-
| 1 |
| x2 |
∵f(x)在区间[1,+∞)上为增函数,
∴f′(x)≥0在[1,+∞)上恒成立,即2a≥
| 1 |
| x3 |
而
| 1 |
| x3 |
| 1 |
| x3 |
∴2a≥1,解得a≥
| 1 |
| 2 |
点评:该题考查函数的奇偶性、单调性的判断,属基础题,熟记相关定义及其基本判断方法是解题关键.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD,PD=2,E为AB的中点.
如图,四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD,PD=2,E为AB的中点.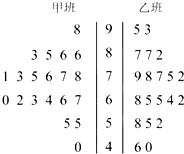 某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.
某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.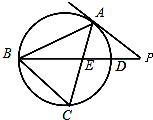 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=