题目内容
8.已知向量$\overrightarrow{{e}_{1}}$=(1,0),$\overrightarrow{{e}_{2}}$=(0,1),动点P从点P0(-1,2)开始沿着与向量$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$相同的方向做匀速直线运动,速度大小为|$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$|;另一动点Q从点Q0(-2,-1)开始沿着与向量3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$相同的方向做匀速直线运动,速度大小为|3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$|,设P、Q在t=0秒时刻分别在P0、Q0处.(1)经过多长时间|PQ|最小?求出最小值;
(2)经过多长时间后$\overrightarrow{PQ}$⊥$\overrightarrow{{P}_{0}{Q}_{0}}$,求出t值.
分析 (1)设经过t秒后P(x1,y1),Q(x2,y2).则$\overrightarrow{{P}_{0}P}$=t($\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}}$).$\overrightarrow{{Q}_{0}Q}$=t($3\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}}$),求出P,Q的坐标,代入距离公式求出最小值;
(2)令$\overrightarrow{PQ}$•$\overrightarrow{{P}_{0}{Q}_{0}}$=0列方程解出t.
解答 解:(1)$\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}}$=(1,1),3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$=(3,2),
设经过t秒后P(x1,y1),Q(x2,y2).则$\overrightarrow{{P}_{0}P}$=(x1+1,y1-2)=t($\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}}$)=(t,t).$\overrightarrow{{Q}_{0}Q}$=(x2+2,y2+1)=t($3\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}}$)=(3t,2t).
∴x1=t-1,y1=t+2,x2=3t-2,y2=2t-1.∴$\overrightarrow{PQ}$=(2t-1,t-3).
∴|$\overrightarrow{PQ}$|2=(2t-1)2+(t-3)2=5t2-10t+10=5(t-1)2+5.
∴当t=1时|$\overrightarrow{PQ}$|2取得最小值5.即|PQ|的最小值为$\sqrt{5}$.
∴出发1秒后|PQ|最小,最小值是$\sqrt{5}$.
(2)$\overrightarrow{{P}_{0}{Q}_{0}}$=(-1,-3),$\overrightarrow{PQ}$•$\overrightarrow{{P}_{0}{Q}_{0}}$=1-2t-3(t-3)=-5t+10.
设t秒后$\overrightarrow{PQ}$⊥$\overrightarrow{{P}_{0}{Q}_{0}}$,则$\overrightarrow{PQ}$•$\overrightarrow{{P}_{0}{Q}_{0}}$=0,∴-5t+10=0,解得t=2.
∴出发2秒后$\overrightarrow{PQ}$⊥$\overrightarrow{{P}_{0}{Q}_{0}}$.
点评 本题考查了平面向量的数量积运算,二次函数的最值,属于中档题.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案| A. | [3,5] | B. | [4,6] | C. | (3,5) | D. | (4,6) |
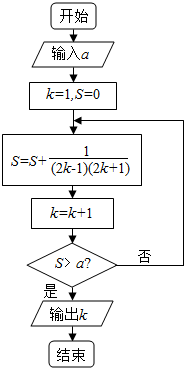 已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )
已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
| A. | 35 | B. | 36 | C. | 120 | D. | 121 |
| A. | 有一个零点 | B. | 有两个零点 | C. | 可能没有零点 | D. | 以上说法不正确 |