题目内容

3．已知函数y=f（x）在区间[1，2]上单调递增，且满足f（1）-f（2）＜0，则f（x）在（1，2）上（　　）
A．有一个零点B．有两个零点C．可能没有零点D．以上说法不正确

分析 对f（x）的最值与0的大小关系进行讨论，得出结论．

解答 解：f（x）是单调递增函数，
（1）若f（1）＜0＜f（2），则f（x）在（1，2）上只有一个零点，
（2）若f（1）＜f（2）＜0或0＜f（1）＜f（2），则f（x）在（1，2）上没有零点，
故选C．

点评 本题考查了函数零点的存在性定理，属于基础题．

练习册系列答案
相关题目
13．已知某几何体直观图和三视图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，
（Ⅰ）求证：BN⊥平面C1B1N；
（Ⅱ）设θ为直线C1N与平面CNB1所成的角，求sinθ的值；
（Ⅲ）设M为AB中点，在BC边上找一点P，使MP∥平面CNB1并求$\frac{BP}{PC}$的值．
14．已知{bn}为单调递增的等差数列，b3+b8=26，b5b6=168，设数列{an}满足$2{a_1}+{2^2}{a_2}+{2^3}{a_3}+…+{2^n}{a_n}={2^{b_n}}$
（1）求数列{bn}的通项；
（2）求数列{an}的前n项和Sn．
11．设x0为函数f（x）=sinπx的零点，且满足|x0|+|f（x0+$\frac{1}{2}$）|＜33，则这样的零点有（　　）
A．61个B．63个C．65个D．67个
18．数列{an}是公差为正数的等差数列，a1+a4=12，a1•a4=27，数列{bn}的前n项和为Tn，且Tn=1-bn（n∈N*）
（1）求数列{an}，{bn}的通项公式；
（2）记cn=an•bn，求数列{cn}的前n项和Sn．
8．已知向量$\overrightarrow{{e}_{1}}$=（1，0），$\overrightarrow{{e}_{2}}$=（0，1），动点P从点P0（-1，2）开始沿着与向量$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$相同的方向做匀速直线运动，速度大小为|$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$|；另一动点Q从点Q0（-2，-1）开始沿着与向量3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$相同的方向做匀速直线运动，速度大小为|3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$|，设P、Q在t=0秒时刻分别在P0、Q0处．
（1）经过多长时间|PQ|最小？求出最小值；
（2）经过多长时间后$\overrightarrow{PQ}$⊥$\overrightarrow{{P}_{0}{Q}_{0}}$，求出t值．
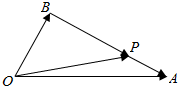15．如图，在△OAB中，已知P为线段AB上一点，$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$．
（1）若$\overrightarrow{BP}$=2$\overrightarrow{PA}$，求x，y的值；
（2）若$\overrightarrow{BP}$=3$\overrightarrow{PA}$，|$\overrightarrow{OA}$|=4，|$\overrightarrow{OB}$|=2，且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°，求$\overrightarrow{OP}$•$\overrightarrow{AB}$的值．
12．（1）已知θ是第二象限角，试判断tan（sinθ）•cot（cosθ）的符号；
（2）若sin（cosθ）•cos（sinθ）＜0，则θ为第几象限角？
13．己知直线2x+y-8=0与直线x-2y+1=0交于点P．
（1）求过点P且平行于直线4x-3y-7=0的直线11的方程；（结果都写成一般方程形式）
（2）求过点P的所有直线中使原点O到此直线的距离最大的直线12的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网