题目内容
已知数列{an}满足an=2an-1+1(n≥2)且a1=1,bn=log2(a2n+1+1),cn=
-1
(Ⅰ)求证:数列{an+1}为等比数列,并求数列{an}的通项公式;
(Ⅱ)求数列{cn}的前n项和sn.
| 1 | ||
|
(Ⅰ)求证:数列{an+1}为等比数列,并求数列{an}的通项公式;
(Ⅱ)求数列{cn}的前n项和sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)把已知的数列递推式an=2an-1+1变形,得到an+1=2(an-1+1)(n≥2),由此得到数列{an+1}为等比数列,求其通项公式后可得数列数列{an}的通项公式;
(Ⅱ)把(Ⅰ)中求得的通项公式代入bn=log2(a2n+1+1),进一步代入cn=
-1,然后由裂项相消法求和.
(Ⅱ)把(Ⅰ)中求得的通项公式代入bn=log2(a2n+1+1),进一步代入cn=
| 1 | ||
|
解答:
(Ⅰ)证明:由an=2an-1+1(n≥2),知an+1=2(an-1+1)(n≥2),
又a1+1=2≠0,
∴{an+1}是以2为首项,以2为公比的等比数列,
故an+1=2•2n-1=2n,
∴an=2n-1;
(Ⅱ)解:由(Ⅰ)知bn=log2(a2n+1+1)=2n+1,
cn=
-1=
=
(
-
),
∴Sn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)=
.
又a1+1=2≠0,
∴{an+1}是以2为首项,以2为公比的等比数列,
故an+1=2•2n-1=2n,
∴an=2n-1;
(Ⅱ)解:由(Ⅰ)知bn=log2(a2n+1+1)=2n+1,
cn=
| 1 | ||
|
| 1 |
| 4n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 4 |
| 1 |
| n+1 |
| n |
| 4(n+1) |
点评:本题考查了数列递推式,考查了等比数列的确定,训练了裂项相消法求数列的和,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知命题p:?m∈R,m+1≤0,命题q:?x∈R,x2+mx+1>0.若“p∧q”为假命题,则实数m的取值范围是( )
| A、(-∞,-2]∪(-1,+∞) |
| B、[2,+∞) |
| C、(-∞,-2]∪[2,+∞) |
| D、[-2,2] |
已知两定点F1(-1,0)、F2(1,0),则命题甲:|F1F2|是|PF1|与|PF2|的等差中项,命题乙:动点P的轨迹是椭圆,则甲是乙的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
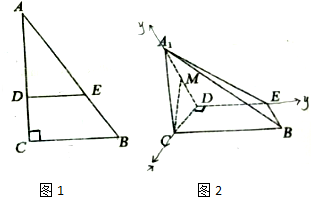 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,DE分别为AC、AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.求证:A1C⊥平面BCDE.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,DE分别为AC、AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.求证:A1C⊥平面BCDE.