题目内容
设函数f(x)=
(Ⅰ)a从集合{1,2,3,4}中任取一个数,b从集合{1,2,3}中任取一个数,求使函数的定义域为全体实数的概率;
(Ⅱ)a从区间[0,4]任取一个数,b从区间[0,3]任取一个数,求使函数有零点的概率.
| x2+2ax+b2 |
(Ⅰ)a从集合{1,2,3,4}中任取一个数,b从集合{1,2,3}中任取一个数,求使函数的定义域为全体实数的概率;
(Ⅱ)a从区间[0,4]任取一个数,b从区间[0,3]任取一个数,求使函数有零点的概率.
考点:几何概型,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)由题意可得,D=R 即△=4a2-4b2<0,即|a|<|b|,由此求得满足此条件的(a,b)共有12个.而所有的(a,b)共有6个,由此求得D=R的概率.
(2)由题意可得,△=4a2-4b2<0,根据a、b的范围,只要|a|<|b|即可.所有的(a,b)构成矩形区域OABC,再画出|b|>|a|的区域,它们相交的部分(即图中阴影部分),再用阴影部分的面积除以矩形OABC的面积,即得所求.
(2)由题意可得,△=4a2-4b2<0,根据a、b的范围,只要|a|<|b|即可.所有的(a,b)构成矩形区域OABC,再画出|b|>|a|的区域,它们相交的部分(即图中阴影部分),再用阴影部分的面积除以矩形OABC的面积,即得所求.
解答:
解:(1)∵a∈{1,2,3,4},b∈{1,2,3},∴(a,b)的所有可能为:
(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3)共计12种. …(2分)
而D=R,有4a2-4b2≤0,即|a|≤|b|…(4分)
那么满足D=R的(a,b)的所有可能为:
(1,1),(1,2),(1,3),((2,2),(2,3),(3,3)共计6种,
∴其概率P=
=
…(6分)
(2)∵a∈[0,4],b∈[0,3]∴所有的点(a,b)构成的区域的面积=12
而有4a2-4b2≥0,即|a|≥|b|…(8分)
满足|a|≥|b|的点(a,b)构成的区域的面积为7.5 …(11分)
故所求概率P=
…(12分)
(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3)共计12种. …(2分)
而D=R,有4a2-4b2≤0,即|a|≤|b|…(4分)
那么满足D=R的(a,b)的所有可能为:
(1,1),(1,2),(1,3),((2,2),(2,3),(3,3)共计6种,
∴其概率P=
| 6 |
| 12 |
| 1 |
| 2 |
(2)∵a∈[0,4],b∈[0,3]∴所有的点(a,b)构成的区域的面积=12
而有4a2-4b2≥0,即|a|≥|b|…(8分)
满足|a|≥|b|的点(a,b)构成的区域的面积为7.5 …(11分)
故所求概率P=
| 5 |
| 8 |
点评:本题考查了几何概型的应用;关键要明确所求事件概率与全部事件的关系,利用区域的长度、面积或者体积之比表示概率.

练习册系列答案
相关题目
如图给出了计算3+5+7+…+19的值的一个程序框图,其中空白处应填入( )


| A、i>9 | B、i>10 |
| C、i>19 | D、i>20 |
对于正整数a,若存在正整数b,使得a=bn(n∈N+)则a是n次方数,其中2次方数也叫平方数,则“正整数a是平方数”是“正整数a是4次方数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
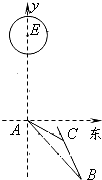 在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20
在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20