Question

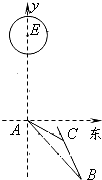在特定时段内，以点E为中心的5海里以内海域被设为警戒水域．点E正南30海里处有一个雷达观测点A．某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20

2

海里的位置B，经过40分钟又测得该船已行驶到点A南偏东45°+θ（其中cosθ=

5

26

，0＜θ＜

π

2

）且与点A相距5

13

海里的位置C．
（1）求该船的行驶速度（单位：海里/时）；
（2）若该船不改变方向继续行驶，判断它是否会进入警戒水域；若会，试求从C点到进入警戒水域，船还要行驶多长时间，若不会，请说明理由．

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：（1）利用余弦定理求出BC，即可求该船的行驶速度；
（2）以A为原点建立平面直角坐标系，求出点E（0，30）到直线BC的距离为d=2

5

＜5所以船会进入警戒水域，求出GC，即可求得结论．

解答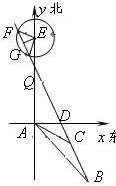： 解：（1）如图：AB=20

2

，AC=5

13

，∠BAC=θ，cosθ=

5

26

，0＜θ＜

π

2

∴sinθ-

1

26

…（1分）
由余弦定理得BC=5

5

…（4分）
所以船的行驶速度为5

5

÷

2

3

=

15 5

2

（海里/小时）…（5分）
（2）如图所示，以A为原点建立平面直角坐标系，
设点B（x₁，y₁），C（x₂，y₂），BC与x轴的交点为D．…（6分）
由题设有，x₁=20，y₁=-20，x₂=ACcos∠CAD=15，y₂=-ABsin∠CAD=-10…（8分）
所以过点B，C的直线l的斜率-2，直线l方程为：y=-2x+20，…（9分）
又点E（0，30）到直线BC的距离为d=2

5

＜5
所以船会进入警戒水域．
又设直线BC上点G（x，20-2x）到点E距离为5．…（10分）
则（x-0）²+（20-2x-30）²=25，
∴x=-3或-5…（11分）
由图形易知G（-3，26），则GC=18

5

…（12分）
所以从C点到进入警戒水域，船还要行驶18

5

÷

15 5

2

=2.4（小时）．…（13分）

点评：本题主要考查正弦定理、余弦定理的应用．考查学生的运算能力、综合考虑问题的能力．