题目内容
已知a2x=
+1,求
的值.
| 2 |
| a3x+a-3x |
| ax+a-x |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:根据指数幂的运算法则将条件进行化简,将条件直接代入即可得到结论.
解答:
解:
=
=a2x-1+a-2x,
∵a2x=
+1,
∴a-2x=(
+1)-1═
=
-1,
∴a2x-1+a-2x=
+1-1+
-1=2
-1,.
即
=2
-1.
| a3x+a-3x |
| ax+a-x |
| (ax+a-x)(a2x-a2x?a-2x+a-2x) |
| ax+a-x |
∵a2x=
| 2 |
∴a-2x=(
| 2 |
| 1 | ||
|
| 2 |
∴a2x-1+a-2x=
| 2 |
| 2 |
| 2 |
即
| a3x+a-3x |
| ax+a-x |
| 2 |
点评:本题主要考查指数幂的化简与求值,利用立方和公式是解决本题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
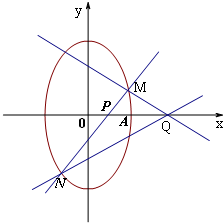 已知椭圆C:
已知椭圆C: