题目内容
为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下2×2列联表:
(1)根据独立性检验的基本思想,约有多大的把握认为“性别与喜欢数学课之间有关系”?
(2)若采用分层抽样的方法从不喜欢数学课的学生中随机抽取5人,则男生和女生抽取的人数分别是多少?
(3)从(2)随机抽取的5人中再随机抽取3人,该3人中女生的人数记为ξ,求ξ的数学期望.
| 喜欢数学课 | 不喜欢数学课 | 合计 | |
| 男 | 30 | 60 | 90 |
| 女 | 20 | 90 | 110 |
| 合计 | 50 | 150 | 200 |
(2)若采用分层抽样的方法从不喜欢数学课的学生中随机抽取5人,则男生和女生抽取的人数分别是多少?
(3)从(2)随机抽取的5人中再随机抽取3人,该3人中女生的人数记为ξ,求ξ的数学期望.
考点:分层抽样方法,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)计算K2的值,根据K2的值大于5.024,可得约有97.5%以上的把握认为“性别与喜欢数学课之间有关系”.
(2)用样本容量乘以男生所占的比例,可得应抽取的男生数,用样本容量乘以女生所占的比例,可得应抽取的女生数.
(3)由(2)可知,男生抽取的人数为2人,女生抽取的人数为3人,所以ξ的取值为1,2,3,再求出ξ取每一个值的概率,即可求得ξ的分布列和数学期望.
(2)用样本容量乘以男生所占的比例,可得应抽取的男生数,用样本容量乘以女生所占的比例,可得应抽取的女生数.
(3)由(2)可知,男生抽取的人数为2人,女生抽取的人数为3人,所以ξ的取值为1,2,3,再求出ξ取每一个值的概率,即可求得ξ的分布列和数学期望.
解答:
解:(1)∵K2=
≈6.061>5.024,
∴约有97.5%以上的把握认为“性别与喜欢数学课之间有关系”.
(2)男生抽取的人数有:
×5=2(人),
女生抽取的人数各有:
×5=3(人).
(3)由(2)可知,男生抽取的人数为2人,女生抽取的人数为3人,所以ξ的取值为1,2,3.
∵P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=3)=
=
,
所以ξ的分布列为:
所以ξ的数学期望为Eξ=1×
+2×
+3×
=1.8.
| 200(30×90-60×20)2 |
| 90×110×50×150 |
∴约有97.5%以上的把握认为“性别与喜欢数学课之间有关系”.
(2)男生抽取的人数有:
| 60 |
| 60+90 |
女生抽取的人数各有:
| 90 |
| 60+90 |
(3)由(2)可知,男生抽取的人数为2人,女生抽取的人数为3人,所以ξ的取值为1,2,3.
∵P(ξ=1)=
| ||||
|
| 3 |
| 10 |
| ||||
|
| 6 |
| 10 |
| ||
|
| 1 |
| 10 |
所以ξ的分布列为:
| ξ | 1 | 2 | 3 | ||||||
| P(ξ) |
|
|
|
| 3 |
| 10 |
| 6 |
| 10 |
| 1 |
| 10 |
点评:本题主要考查独立性检验、分层抽样、离散型随机变量的分布列与数学期望,属于中档题.

练习册系列答案
相关题目
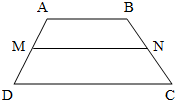 用向量法证明:梯形的中位线平行于两底边且等于两底边和的一半.
用向量法证明:梯形的中位线平行于两底边且等于两底边和的一半.