题目内容
设x，y满足约束条件组
，若目标函数z=ax+by（a＞0，b＞0）的最大值为24，则
+
的最小值为（ ）
|
| 4 |
| a |
| 6 |
| b |
A、
| ||
B、
| ||
| C、4 | ||
D、
|
考点：简单线性规划
专题：不等式的解法及应用
分析：已知2a+3b=6，求则
+
的最小值，可以作出不等式的平面区域，先用乘积进而用基本不等式解答．
| 4 |
| a |
| 6 |
| b |
解答：
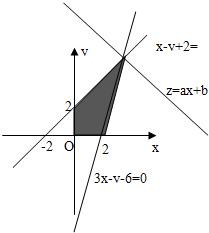解：不等式表示的平面区域如图所示阴影部分，
当直线ax+by=z（a＞0，b＞0）
过直线x-y+2=0与直线3x-y-6=0的交点（4，6）时，
目标函数z=ax+by（a＞0，b＞0）取得最大24，
即4a+6b=24，即2a+3b=12，而则
+
=（
+
）
=
+
+
≥
+2=
，当且仅当a=b=
取等号，
故则
+
的最小值为
，
故选：D．
解：不等式表示的平面区域如图所示阴影部分，当直线ax+by=z（a＞0，b＞0）
过直线x-y+2=0与直线3x-y-6=0的交点（4，6）时，
目标函数z=ax+by（a＞0，b＞0）取得最大24，
即4a+6b=24，即2a+3b=12，而则
| 4 |
| a |
| 6 |
| b |
| 4 |
| a |
| 6 |
| b |
| 2a+3b |
| 12 |
| 13 |
| 6 |
| b |
| a |
| a |
| b |
| 13 |
| 6 |
| 25 |
| 6 |
| 12 |
| 5 |
故则
| 4 |
| a |
| 6 |
| b |
| 25 |
| 6 |
故选：D．
点评：本题综合地考查了线性规划问题和由基本不等式求函数的最值问题．要求能准确地画出不等式表示的平面区域，并且能够求得目标函数的最值．
练习册系列答案
相关题目
p=
+
，q=
•
（m、n、a、b、c、d均为正数），则p、q的大小为（ ）
| ab |
| cd |
| ma+nc |
|
| A、p≥q | B、p≤q |
| C、p＞q | D、不确定 |
关于x的方程x2+（m-2）x+5-m=0的两根均大于2，则实数m的取值范围是（ ）
| A、（-5，-4] |
| B、（-∞，-5）∪（-5，-4） |
| C、（-∞，-4] |
| D、（-∞，-2） |
数列{an}中，a1=1，对所有的n≥2都有a1a2…an=n2，则a4•a5=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在平行四边形ABCD中，
+
+
=（ ）
| AB |
| CA |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
6名医生被分配到6所学校为学生体检，每校分配一名医生，则不同的分配方法有（ ）
| A、6种 | B、720种 |
| C、120种 | D、12种 |
已知a，b是两条不同的直线，α，β，γ是三个不同的平面，下列命题中正确的是（ ）
| A、若a∥α，b∥α，则a∥b |
| B、若a，b与α所成的角相等，则a∥b |
| C、若α⊥γ，β⊥γ，则α∥β |
| D、若a⊥α，a⊥β，则α∥β |