题目内容
5．已知$tanα=\frac{1}{2}$，则cos2α=（ ）| A． | $\frac{2}{5}$ | B． | $\frac{3}{5}$ | C． | $±\frac{2}{5}$ | D． | $±\frac{3}{5}$ |
分析 由条件利用二倍角的余弦公式，求得要求式子的值．
解答 解：cos2α=cos2α-sin2α=$\frac{co{s}^{2}α-si{n}^{2}α}{co{s}^{2}α+si{n}^{2}α}$=$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$=$\frac{1-\frac{1}{4}}{1+\frac{1}{4}}$=$\frac{3}{5}$，
故选：B．
点评 本题主要考查二倍角的余弦公式的应用，属于基础题．
练习册系列答案
相关题目
16．抛物线y=x2上到直线2x-y-4=0距离最近的点的坐标是（ ）
| A． | （1，1） | B． | $（{\frac{1}{2}，\frac{1}{4}}）$ | C． | $（{\frac{1}{3}，\frac{1}{9}}）$ | D． | （2，4） |
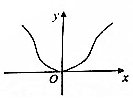
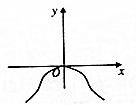
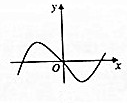
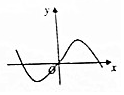
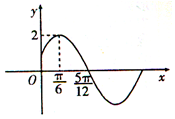已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，$-\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示．