题目内容
3.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,点P(3,$\frac{5}{2}$)为双曲线上一点,若△PF1F2的内切圆的半径为1,则双曲线的方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1.分析 运用三角形面积的等积法,两次求得△PF1F2的面积,可得|PF1|+|PF2|=3c,再由双曲线的定义,可得|PF1|,|PF2|,再由两点的距离公式,解得a=2,将P的坐标代入双曲线的方程,解方程可得b,进而得到双曲线的方程.
解答 解:点P(3,$\frac{5}{2}$)为双曲线上一点,
可得S${\;}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}$|F1F2|•yP=$\frac{1}{2}$•2c•$\frac{5}{2}$=$\frac{5}{2}$c,
△PF1F2的内切圆的半径为1,
可得S${\;}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}$(|PF1|+|PF2|+|F1F2|)•1=$\frac{1}{2}$(|PF1|+|PF2|+2c),
可得|PF1|+|PF2|=3c,
由双曲线的定义可得|PF1|-|PF2|=2a,
解得|PF1|=$\frac{3c+2a}{2}$,|PF2|=$\frac{3c-2a}{2}$,
又|PF1|=$\sqrt{(3+c)^{2}+\frac{25}{4}}$,|PF2|=$\sqrt{(3-c)^{2}+\frac{25}{4}}$,
联立化简得a=2.
又因点点P(3,$\frac{5}{2}$)在双曲线上,
所以$\frac{9}{4}$-$\frac{25}{4{b}^{2}}$=1,解得b=$\sqrt{5}$,
故双曲线方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1.
故答案为:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1.
点评 本题考查双曲线的定义、方程和性质,主要是定义法的运用和点满足双曲线的方程,考查化简整理的运算能力,属于中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | (1,+∞) | B. | (e,+∞) | C. | (-∞,-1) | D. | (-∞,-e) |
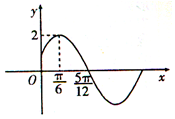 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.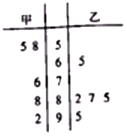 某校拟举办“成语大赛”,高一(1)班的甲、乙两名同学在本班参加:“成语大赛”选拔测试,在相同的测试条件下,两人5次测试的成绩(单位:分)的茎叶图如图所示:
某校拟举办“成语大赛”,高一(1)班的甲、乙两名同学在本班参加:“成语大赛”选拔测试,在相同的测试条件下,两人5次测试的成绩(单位:分)的茎叶图如图所示: