题目内容
4.同时具有以下性质:“①最小正周期是π;②图象关于直线x=$\frac{π}{3}$对称;③在$[-\frac{π}{6},\frac{π}{3}]$上是增函数;④一个对称中心为$(\frac{π}{12},0)$”的一个函数是( )| A. | $y=sin(\frac{x}{2}+\frac{π}{6})$ | B. | $y=sin(2x+\frac{π}{3})$ | C. | $y=sin(2x-\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{3})$ |
分析 根据题意,求解出ω和φ,考查在$[-\frac{π}{6},\frac{π}{3}]$上是增函数;一个对称中心为$(\frac{π}{12},0)$可得答案.
解答 解:由“①最小正周期是π,可得ω=2,排除A;
②图象关于直线x=$\frac{π}{3}$对称;可得:$\frac{2π}{3}$+φ=$\frac{π}{2}+kπ$,k∈Z.
对于D选项:φ=-$\frac{π}{3}$,不满足,排除D;
④一个对称中心为$(\frac{π}{12},0)$”带入函数y中,B选项不满足.排除B;
故选C.
点评 本题主要考查三角函数的图象和性质,同时满足题意的函数很多,所以利用排除法解决比较好.属于基础题.

练习册系列答案
相关题目
12.已知函数f(x)=$\left\{\begin{array}{l}{e^x},x≥0\\ ax,x<0\end{array}$若方程f(-x)=f(x)有五个不同的实根,则实数a的取值范围( )
| A. | (1,+∞) | B. | (e,+∞) | C. | (-∞,-1) | D. | (-∞,-e) |
19.随着经济社会的发展,消费者对食品安全的关注度越来越高,通过随机询问某地区110名居民在购买食品时是否看生产日期与保质期等内容,得到如下的列联表:
年龄与看生产日期与保质期列联表 单位:名
(1)从这50名60岁以上居民中按是否看生产日期与保质期采取分层抽样,抽取一个容量为5的样本,问样本中看与不看生产日期与保质期的60岁以上居民各有多少名?
(2)从(1)中的5名居民样本中随机选取两名作深度访谈,求选到看与不看生产日期与保质期的60岁以上居民各1名的概率;
(3)根据以上列联表,问有多大把握认为“年龄与在购买食品时看生产日期与保质期”有关?
附:下面的临界值表供参考:
年龄与看生产日期与保质期列联表 单位:名
| 60岁以下 | 60岁以上 | 总计 | |
| 看生产日期与保质期 | 50 | 30 | 80 |
| 不看生产日期与保质期 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)从(1)中的5名居民样本中随机选取两名作深度访谈,求选到看与不看生产日期与保质期的60岁以上居民各1名的概率;
(3)根据以上列联表,问有多大把握认为“年龄与在购买食品时看生产日期与保质期”有关?
附:下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
16.△ABC的内角A,B,C的对边分别是a,b,c,满足a2+bc≤b2+c2,则角A的范围是( )
| A. | $(0,\frac{π}{6}]$ | B. | $(0,\frac{π}{3}]$ | C. | $[\frac{π}{6},π)$ | D. | $[\frac{π}{3},π)$ |
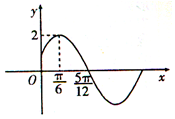 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.