题目内容
已知a，b＞0，实数x，y满足不等式组
，则当
+
取得最小值时，z=bx+ay取最大值的最优解为（ ）
|
| 2a |
| a+b |
| b |
| a |
| A、（0，0） | ||||
| B、（1，0） | ||||
| C、（0，1） | ||||
D、（
|
考点：简单线性规划
专题：不等式的解法及应用
分析：根据基本不等式求出当
+
取得最小值时的等价条件，利用线性规划的知识，利用数形结合，即可得到结论．
| 2a |
| a+b |
| b |
| a |
解答：
解：∵a，b＞0，
∴
+
=
+
+1-1=
+
-1≥2
-1=2
-1，
当且仅当
=
，即（a+b）2=2a2时取等号，即a+b=
a，
则b=（
-1）a，则
=
-1，
由z=bx+ay得y=-
x+
=（1-
）x+
，
作出不等式组对应的平面区域，平移直线y=（1-
）x+
，
则当直线经过点A（0，1）时，直线y=（1-
）x+
的截距最大，
此时最优解为（0，1），
故选：C．
解：∵a，b＞0，∴
| 2a |
| a+b |
| b |
| a |
| 2a |
| a+b |
| b |
| a |
| 2a |
| a+b |
| a+b |
| a |
|
| 2 |
当且仅当
| 2a |
| a+b |
| a+b |
| a |
| 2 |
则b=（
| 2 |
| b |
| a |
| 2 |
由z=bx+ay得y=-
| b |
| a |
| z |
| a |
| 2 |
| z |
| a |
作出不等式组对应的平面区域，平移直线y=（1-
| 2 |
| z |
| a |
则当直线经过点A（0，1）时，直线y=（1-
| 2 |
| z |
| a |
此时最优解为（0，1），
故选：C．
点评：本题主要考查线性规划的应用，利用基本不等式求出当
+
取得最小值的条件，利用数形结合是解决本题的关键，综合性较强，有一定的难度．
| 2a |
| a+b |
| b |
| a |
练习册系列答案
相关题目
已知随机变量X服从正态分布N（3，1），且P（2≤X≤4）=0.6826，则P（X＜2）=（ ）
| A、0.1588 |
| B、0.1587 |
| C、0.1586 |
| D、0.1585 |
对任意两实数a，b，定义运算“*”：a*b=
，关于函数f（x）=e-x*ex-1给出下列四个结论：
①函数f（x）为偶函数；
②函数f（x）的最小值是
③函数f（x）在（0，+∞）上单调递增
④函数f（x）的图象与直线y=e（x+1）有公共点
其中正确结论的序号是（ ）
|
①函数f（x）为偶函数；
②函数f（x）的最小值是
| 1 | ||
|
③函数f（x）在（0，+∞）上单调递增
④函数f（x）的图象与直线y=e（x+1）有公共点
其中正确结论的序号是（ ）
| A、①③ | B、②③ | C、①④ | D、②④ |
设P是不等式组
表示的平面区域内的任意一点，向量
=（1，1），
=（2，1），若
=λ
+μ
（λ，μ为实数），则λ-μ的最大值为（ ）
|
| m |
| n |
| OP |
| m |
| n |
| A、4 | B、3 | C、-1 | D、-2 |
(x-
y)8的展开式中x6y2项的系数是（ ）
| 2 |
| A、56 | B、-56 |
| C、28 | D、-28 |
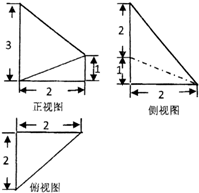
已知某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、8 | ||
B、
| ||
| C、4 | ||
| D、12 |
学校或班级举行活动，通常需要张贴海报进行宣传．现让你设计一张如图所示的竖向张贴的海报，要求版心面积为128dm2，上、下两边各空2dm，左、右两边各空1dm．如何设计海报的尺寸，才能使四周空白面积最小？