题目内容

求由曲线y=x2，y=
1
x
及x=2所围成的平面图形的面积．
考点：定积分在求面积中的应用
专题：导数的概念及应用
分析：作出对应的区域，利用积分即可求出面积．
解答： 解：由
y=x2
y=
1
x
，解得
x=1
y=1
，
则由积分的几何意义可知，所求的区域面积S=
∫
2
1
(x2-
1
x
)dx=（
1
3
x3-lnx）|
 
2
1
=
8
3
-ln2-（
1
3
-ln1）
=
7
3
-ln2．
点评：本题主要考查积分的应用，要求熟练掌握常见函数的积分．
练习册系列答案
相关题目
已知a，b＞0，实数x，y满足不等式组
x+2y≤2
2x+y≤2
x≥0，y≥0
，则当
2a
a+b
+
b
a
取得最小值时，z=bx+ay取最大值的最优解为（　　）
A、（0，0）
B、（1，0）
C、（0，1）
D、（
2
3
，
2
3
）
解下列关于x的方程：
（1）2sinx+cosx=2；
（2）sin2x=sin2x；
（3）cosx+2=2tan2（
x
2
）
设函数f（x）=sin（2x+
π
6
）+cos2x+
3
sinxcosx．
（1）若|x|＜
π
4
，求函数f（x）的值域；
（2）设A，B，C为△ABC的三个内角，若f（
A
2
）=
5
2
，cos（A+C）=-
5
3
14
，求cosC的值．
已知函数f（x）=x（x+a）-lnx，其中a为常数．
（1）求f（x）的单调区间；
（2）问过坐标原点可以作几条直线与曲线y=f（x）相切？并说明理由；
（3）若g（x）=f（x）•e-x在区间（0，1）内是单调函数，求a的取值范围．
在平面直角坐标系xOy中，圆C：（x-2）2+（y-b）2=r2经过点（1，0），且圆C被x轴和y轴截得的弦长之比为1：
6
，求圆的方程．
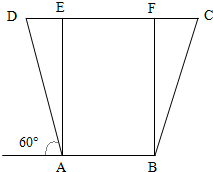如图，水渠的横截面积是等腰梯形，下底及两边坡的总长度为a，坡AD的倾角为60°，
（1）求横截面的面积y与下底AB的宽x之间的函数解析式；
（2）若x∈[
a
4
，
a
2
]，求y的最大值和最小值．
已知命题p：函数f（x）=
1
3
x3+x2+mx+1有两个不同的极值点；命题q：函数f（x）=x2-mx+3在区间[-1，2]是单调减函数．若p且￢q为真命题，求实数m的取值范围．
样本容量为100的频率分布直方图如图所示，由此估计样本数据落在[6，10]内的频数为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网