题目内容
4.已知直三棱柱ABC-A′B′C中,底面是以AC为斜边的等腰直角三角形,且AA′=AB,求异面直线AB′与BC′所成角.分析 以B为原点,BA为x轴,BC为y轴,BB′为z轴,建立空间直角坐标系,利用向量法能求出异面直线AB′与BC′所成角.′
解答 以B为原点,BA为x轴,BC为y轴,BB′为z轴,建立空间直角坐标系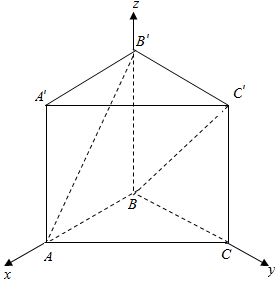
设AA1=AB=1,AA′=t,
则A(1,0,0),B′(0,0,t),B(0,0,0),C′(0,1,0),
$\overrightarrow{A{B}^{'}}$=(-1,0,t),$\overrightarrow{B{C}^{'}}$=(0,1,0),
设异面直线AB′与BC′所成角为θ.
cosθ=$\frac{|\overrightarrow{A{B}^{'}}•\overrightarrow{B{C}^{'}}|}{|\overrightarrow{A{B}^{'}}|•|\overrightarrow{B{C}^{'}}|}$=0,⑥
∴θ=90°,
∴异面直线AB′与BC′所成角为90°.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
14.已知{an}是首项为1的等比数列,若Sn是{an}的前n项和,且28S3=S6,则数列{$\frac{1}{{a}_{n}}$}的前4项和为( )
| A. | $\frac{15}{8}$ | B. | 4 | C. | $\frac{40}{27}$ | D. | 40 |
19.(1-x2)4($\frac{x+1}{x}$)5的展开式中$\frac{1}{x}$的系数为( )
| A. | 5 | B. | 11 | C. | -21 | D. | -29 |
9.若m,n表示不同直线,α,β表示不同的平面,则下列结论中正确的是( )
| A. | 若m∥α,m∥n,则n∥α | B. | 若m?α,n?β,m∥β,n∥α,则α∥β | ||
| C. | 若α⊥β,m∥α,n∥β,则m∥n | D. | 若α∥β,m∥α,n∥m,n?β,则n∥β |
16.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+2≥0}\\{x-y+3≥0}\\{2x+y-3≤0}\end{array}\right.$,则目标函数z=x+2y的最大值为( )
| A. | 0 | B. | 3 | C. | 6 | D. | 12 |
13.从8个学生(其中男生和女生人数相等)中任选3个作为学校元旦晚会的主持人,则男生甲和女生乙恰好同时人选的概率为( )
| A. | $\frac{5}{28}$ | B. | $\frac{9}{56}$ | C. | $\frac{1}{7}$ | D. | $\frac{3}{28}$ |