题目内容
12.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{5π}{6}$.分析 根据向量的数量积公式和向量垂直即可求出.
解答 解:∵($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{a}$=${\overrightarrow{a}}^{2}$+$\overrightarrow{a}$•$\overrightarrow{b}$=${\overrightarrow{a}}^{2}$+|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=3+2$\sqrt{3}$cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=0,
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=-$\frac{\sqrt{3}}{2}$,
∵向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角的范围[0,π]
∴向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角为$\frac{5π}{6}$
故答案为:$\frac{5π}{6}$.
点评 本题考查了向量的数量积公式和向量垂直的条件,属于基础题.

练习册系列答案
相关题目
2.函数$f(x)=\sqrt{3}sinx+sin(\frac{π}{2}+x)$的一条对称轴是( )
| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{2π}{3}$ | D. | $x=\frac{5π}{6}$ |
3.已知全集U={0,1,2,3,4,5,6},集合A={0,1,3},集合B={2,6},则(∁UA)∩(∁UB)为( )
| A. | {5,6} | B. | {4,5} | C. | {0,3} | D. | {2,6} |
20.如图,在正六边形ABCDEF中,|$\overrightarrow{AC}$+$\overrightarrow{AE}$|=6,则$\overrightarrow{AF}$•$\overrightarrow{FB}$等于( )
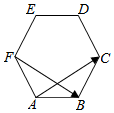

| A. | -6 | B. | 6 | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
7.已知直线ax+by=1经过点(1,2),则2a+4b的最小值为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
17.若复数z满足(1+2i)2z=1-2i,则共轭复数$\overline{z}$为( )
| A. | $\frac{11}{25}$+$\frac{2}{25}$i | B. | -$\frac{11}{25}$-$\frac{2}{25}$i | C. | -$\frac{11}{25}$+$\frac{2}{25}$i | D. | $\frac{11}{25}$-$\frac{2}{25}$i |
1.已知|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,则满足条件|m$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{33}$的所有实数m之和为( )
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |