题目内容
5.若圆x2+y2=1与圆x2+y2+6x-8y+m=0相切,则m的值为-11或9.分析 由题意,两个圆相内切,根据两圆的圆心距等于两圆的半径之差的绝对值,两个圆相外切,两圆的圆心距等于半径之和,求得m的值.
解答 解:圆x2+y2+6x-8y+m=0 即(x+3)2+(y-4)2=25-m,
表示以(-3,4)为圆心,半径等于$\sqrt{25-m}$的圆.
由题意,两个圆相内切,两圆的圆心距等于半径之差的绝对值,
可得5=|$\sqrt{25-m}$-1|,
解得m=-11.
两个圆相外切,两圆的圆心距等于半径之和,可得5=$\sqrt{25-m}$+1,
解得m=9,
故答案为:-11或9.
点评 本题主要考查圆的标准方程的特征,两点间的距离公式,两圆的位置关系的判定方法,属于中档题.

练习册系列答案
相关题目
15.已知集合A={1,3,5},B={1,m},A∩B={1,m},则m等于( )
| A. | 1 或 3 | B. | 3 或 5 | C. | 1 或 5 | D. | 1 或 3 或5 |
20.方程$|x|-2=\sqrt{4-{{({y-2})}^2}}$表示的曲线是( )
| A. | 一个圆 | B. | 半圆 | C. | 两个圆 | D. | 两个半圆 |
10.如果直线l将圆x2+y2+2x-4y=0平分,且不过第一象限,那么l的斜率的取值范围是( )
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,-2] |
17.设△ABC的内角A,B,C所对的边长分别为a,b,c,若bcosC+ccosB=2acosA,则A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
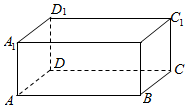 如图,长方体ABCD-A1B1C1D1中,AB=12,BC=10,AA1=8,过点A1、D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.
如图,长方体ABCD-A1B1C1D1中,AB=12,BC=10,AA1=8,过点A1、D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.