题目内容
17．若函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1，x＜3}\\{lo{g}_{3}x，x≥3}\end{array}\right.$，则f（f（9））=5．分析 利用分段函数转化求解函数值即可．
解答 解：函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1，x＜3}\\{lo{g}_{3}x，x≥3}\end{array}\right.$，则f（f（9））=f（log39）=f（2）=22+1=5．
故答案为：5．
点评 本题考查分段函数的应用，函数值的求法，考查计算能力．
练习册系列答案
相关题目
12．圆x2+y2+4x-2y+$\frac{24}{5}$=0上的点到直线3x+4y=0的距离的最大值是（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{1}{5}$ | C． | $\frac{2+\sqrt{5}}{5}$ | D． | $\frac{2-\sqrt{5}}{5}$ |
如图，点A的坐标为（1，0），函数y=ax2过点C（2，4），若在矩形ABCD内随机取一点，则此点取自阴影部分的概率等于$\frac{5}{12}$．
6．函数y=x3+x+1递增区间是（ ）
| A． | （0，+∞） | B． | （-∞，1） | C． | （-∞，+∞） | D． | （1，+∞） |
7．
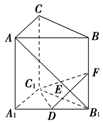直三棱柱ABC-A1B1C1中，侧棱长为2，AC=BC=1，∠ACB=90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E，要使AB1⊥平面C1DF，则线段B1F的长为（ ）
直三棱柱ABC-A1B1C1中，侧棱长为2，AC=BC=1，∠ACB=90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E，要使AB1⊥平面C1DF，则线段B1F的长为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |