题目内容

8．若sinα（1+$\sqrt{3}$tan10°）=1，则钝角α=140°．

分析 利用同角三角函数基本关系、诱导公式，可得sinα=cos40°，结合α为钝角，可得α的值．

解答 解：sinα（1+$\sqrt{3}$tan10°）=sinα•$\frac{cos10°+\sqrt{3}sin10°}{cos10°}$=sinα•2•$\frac{sin40°}{cos10°}$=1，
∴2sinα•sin40°=cos10°=sin80°，
即2sinα•sin40°=sin80°，∴sinα=cos40°，结合α为钝角，可得α=140°，
故答案为：140°．

点评 本题主要考查同角三角函数基本关系、诱导公式的运用，属于基本知识的考查．

练习册系列答案
相关题目
2．某化肥厂生产甲、乙两种混合肥料，需要A，B，C三种主要原料，生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示：
肥料  原料ABC
甲483
乙5510
现有A种原料200吨，B种原料360吨，C种原料300吨，在此基础上生产甲、乙两种肥料．已知生产1车皮甲种肥料，产生的利润为2万元；生产1车皮乙种肥料，产生的利润为3万元、分别用x，y表示计划生产甲、乙两种肥料的车皮数．
（Ⅰ）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（Ⅱ）问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润．
19．直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为$ρ=2\sqrt{2}sin（θ+\frac{π}{4}）$，直线l的参数方程为$\left\{{\begin{array}{l}{x=1-\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$（t为参数），直线l与曲线C1交于A，B两点．
（Ⅰ）求|AB|的长度；
（Ⅱ）若曲线C2的参数方程为$\left\{{\begin{array}{l}{x=3+\sqrt{2}cosα}\\{y=4+\sqrt{2}sinα}\end{array}}\right.$（α为参数），P为曲线C2上的任意一点，求△PAB的面积的最小值．
16．若数列{an}满足an-2an+1+an+2=0（n∈N*），且a1=2，a2=4，则数列{an}的通项公式为an=2n．
3．设集合A为函数y=lg$\frac{1+x}{2-x}$的定义域，集合B为不等式（ax-1）（x+2）≥0（a＞0）的解集．
（1）若a=1，求A∩B；
（2）若B⊆∁RA，求实数a的取值范围．
13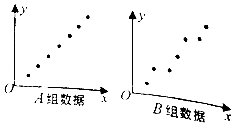．如图，给出了样本容量均为7的A、B两组样本数据的散点图，已知A组样本数据的相关系数为r1，B组数据的相关系数为r2，则（　　）
A．r1＞r2＞0B．r2＞r1＞0C．r1＜r2＜0D．r2＜r1＜0
20．方程3sinx=1+cos2x的解集为$\{x|x=kπ+{（-1）^k}•\frac{π}{6}\}，k∈Z$．
17．若函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1，x＜3}\\{lo{g}_{3}x，x≥3}\end{array}\right.$，则f（f（9））=5．
18．计算$\int_0^2{（{\sqrt{4-{x^2}}-2x}）dx=}$（　　）
A．2π-4B．π-4C．ln2-4D．ln2-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网